Vibration, Shock,
and Acoustics

Engineering Cheat Sheet

Ref: VSA-2025-G

01. Core Acoustics & dB Fundamentals

Sound Pressure Level (SPL)

Logarithmic measure of effective sound pressure relative to a reference value.

L_p = 20 \log_{10} \left( \frac{p_{rms}}{p_{ref}} \right) \text{ dB}

$p_{rms}$ = root mean square sound pressure
$p_{ref}$ = reference sound pressure

Medium	Reference Pressure	Notes
Air	$p_{ref} = 20 \mu\text{Pa}$	Threshold of human hearing at 1 kHz
Water	$p_{ref} = 1 \mu\text{Pa}$	Underwater acoustics standard (ISO)

Conversion: To convert air SPL to water SPL scale: add

26 \text{ dB}

(since

20\log_{10}(20/1) = 26

). Note: This is only a reference shift, not a physical equivalence.

Wave Equation

Governs propagation of acoustic pressure disturbances through a medium.

\nabla^2 p - \frac{1}{c^2}\frac{\partial^2 p}{\partial t^2} = 0

1D Form

\frac{\partial^2 p}{\partial x^2} = \frac{1}{c^2}\frac{\partial^2 p}{\partial t^2}

Speed of Sound

c = \sqrt{\frac{\gamma R T}{M}} \approx 343 \text{ m/s}

at 20°C in air

$p$ = acoustic pressure (Pa)
$c$ = speed of sound (m/s)
$\nabla^2$ = Laplacian operator

Plane Wave Solution:

p(x,t) = A e^{i(\omega t - kx)} + B e^{i(\omega t + kx)}

where

k = \omega/c

is the wavenumber.

Ref: Kinsler et al. "Fundamentals of Acoustics" Wiley 2000; Beranek & Mellow "Acoustics: Sound Fields and Transducers" Academic Press 2012

02. SDOF Dynamics

SDOF Calculator

m\ddot{x} + c\dot{x} + kx = F_0 \sin(\omega t)

Natural Frequency

\omega_n = \sqrt{\frac{k}{m}}

f_n = \frac{1}{2\pi}\sqrt{\frac{k}{m}}

Damping Ratio

\zeta = \frac{c}{2\sqrt{km}}

Dynamic Magnification Factor (DMF)

Ratio of dynamic response amplitude to static deflection under the same force magnitude.

DMF = \frac{X}{X_{static}} = \frac{1}{\sqrt{(1-r^2)^2 + (2\zeta r)^2}}

$r = \omega / \omega_n$ = frequency ratio
$X_{static} = F_0/k$ = static deflection

r ≪ 1
DMF ≈ 1
Stiffness controlled

r = 1
DMF = Q = 1/(2ζ)
Resonance (max)

r ≫ 1
DMF ≈ 1/r²
Mass controlled

Phase Angle ( $\phi$ )

\phi = \tan^{-1} \left( \frac{2\zeta r}{1-r^2} \right)

$r \ll 1$ : $\phi \approx 0^\circ$ (Stiffness controlled)
$r = 1$ : $\phi = 90^\circ$ (Resonance)
$r \gg 1$ : $\phi \approx 180^\circ$ (Mass controlled)

Transmissibility

Base excitation to response:

T(\omega) = \sqrt{\frac{1 + (2\zeta r)^2}{(1-r^2)^2 + (2\zeta r)^2}}

Ref: Rao "Mechanical Vibrations" Pearson 2017; Thomson & Dahleh "Theory of Vibration with Applications" Prentice Hall 1998

03. Damping Types

Viscous Damping

Force proportional to velocity. Ideal for fluids/dashpots.

F_d = -c \dot{x}

Structural (Hysteretic) Damping

Energy dissipated per cycle is independent of frequency. Used for solids/metals.

F_d = -i \eta k x

$\eta = 2\zeta$ (at resonance)

Coulomb (Dry Friction) Damping

Constant force opposing motion.

F_d = -\mu N \text{ sgn}(\dot{x})

Q Factor & Loss Factor

Q = \frac{1}{2\zeta} = \frac{1}{\eta}

Valid for light damping ( $\zeta < 0.1$ ).

Ref: Nashif et al. "Vibration Damping" Wiley 1985; Jones "Handbook of Viscoelastic Vibration Damping" Wiley 2001

04. MDOF Dynamics

2-DOF Calculator

Matrix Equation of Motion

[M]\{\ddot{x}\} + [C]\{\dot{x}\} + [K]\{x\} = \{F(t)\}

$[M]$ = Mass matrix (n×n)
$[C]$ = Damping matrix (n×n)
$[K]$ = Stiffness matrix (n×n)
$\{x\}$ = Displacement vector (n×1)

Eigenvalue Problem (Free Vibration)

([K] - \omega_n^2 [M])\{\phi\} = \{0\}

Yields n natural frequencies $\omega_{n,i}$ and mode shapes $\{\phi_i\}$ .

Damping Treatment: The eigenvalue problem is solved for the undamped system (C=0). Damping is typically added later via modal damping ratios

\zeta_i

assigned to each mode, or through proportional (Rayleigh) damping:

[C] = \alpha[M] + \beta[K]

where

\zeta_i = \frac{\alpha}{2\omega_i} + \frac{\beta\omega_i}{2}

Modal Superposition

Transform to modal coordinates $\{q\}$ :

\{x\} = [\Phi]\{q\}

Where $[\Phi]$ = modal matrix (columns are mode shapes).

Modal Coordinates $q_i$ : Each

q_i(t)

is a scalar "participation factor" that scales how much mode

i

contributes to the total response at time

t

. Physical displacement = sum of mode shapes weighted by their modal coordinates.

Decoupled Equations:

\ddot{q}_i + 2\zeta_i \omega_{n,i} \dot{q}_i + \omega_{n,i}^2 q_i = \frac{\{\phi_i\}^T\{F\}}{m_i}

Modal Vector Interpretation

A mode shape $\{\phi_i\}$ describes the relative displacement pattern when the system vibrates at frequency $\omega_{n,i}$ .

Amplitude meaning: Only the ratio between DOFs matters, not absolute values. Mode shapes are typically normalized (mass-normalized: $\{\phi\}^T[M]\{\phi\}=1$ , or max=1.0).
Sign: Positive/negative indicates in-phase/out-of-phase motion between DOFs.
Zero crossings: Nodes where that DOF has no motion for that mode.

Ref: Meirovitch "Fundamentals of Vibrations" McGraw-Hill 2001; Ewins "Modal Testing: Theory, Practice and Application" Wiley 2000

05. Force Balance (Beam Theory)

Beam Calculator

Euler-Bernoulli Beam Equation: $EI \frac{d^4w}{dx^4} = q(x)$

Relationships

Shear Force (V)

V(x) = \frac{dM}{dx}

Bending Moment (M)

M(x) = EI \frac{d^2w}{dx^2}

Force/Moment Balance

Force Balance:

\sum F_y = 0: V - (V + dV) + q \cdot dx = 0

\Rightarrow \frac{dV}{dx} = q(x)

Moment Balance:

\sum M = 0: dM = V \cdot dx

\Rightarrow \frac{dM}{dx} = V(x)

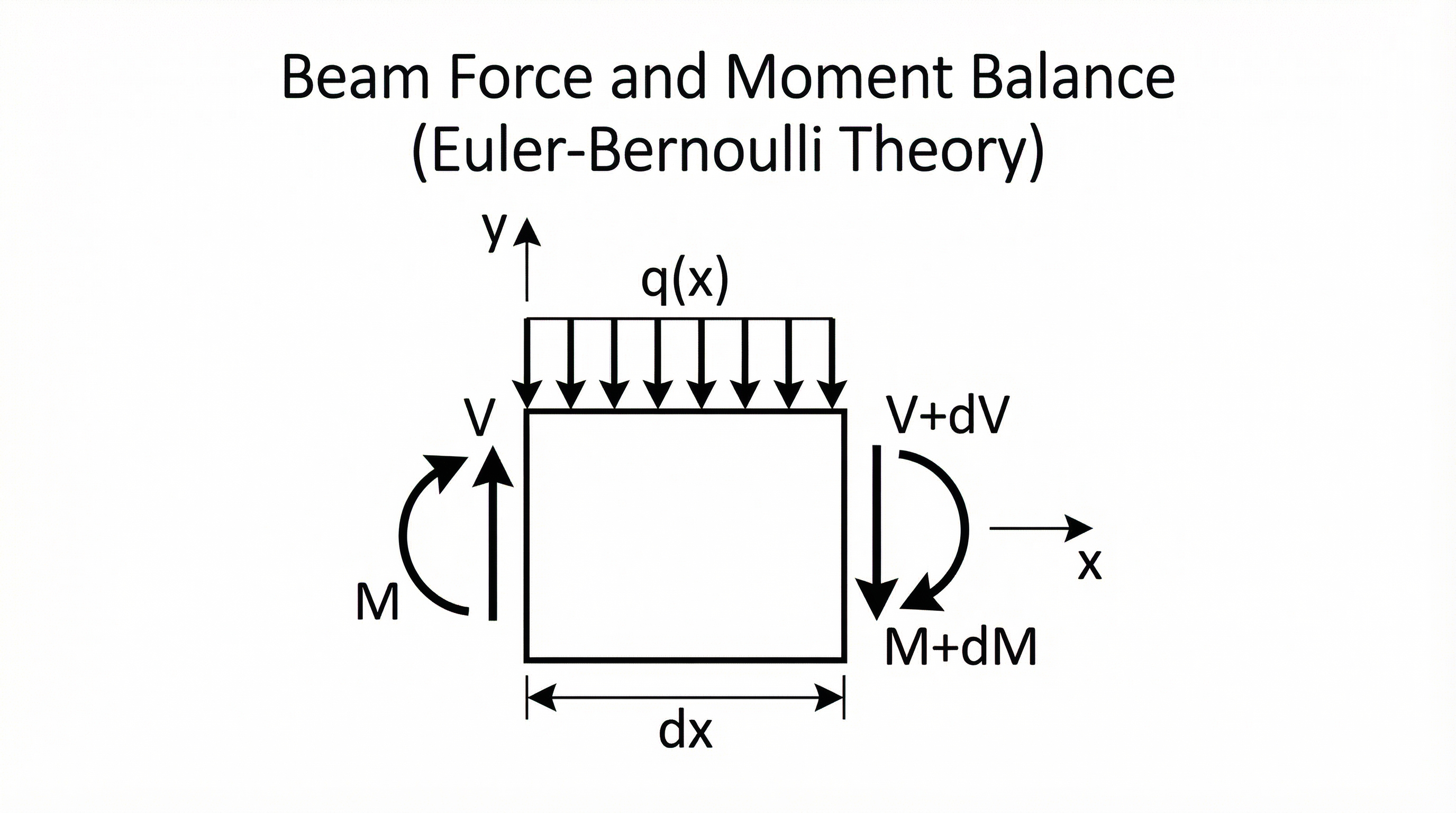
Boundary Conditions

Type	Deflection ( $w$ )	Slope ( $w'$ )	Moment ( $M$ )	Shear ( $V$ )
Fixed	0	0	$\neq 0$	$\neq 0$
Pinned	0	$\neq 0$	0	$\neq 0$
Free	$\neq 0$	$\neq 0$	0	0

Ref: Timoshenko & Gere "Mechanics of Materials" PWS 1997; Gere & Goodno "Mechanics of Materials" Cengage 2018

06. Random Vibration

G-RMS Tool

Miles' Equation

Estimates RMS response of SDOF system to flat random input.

\ddot{x}_{rms} = \sqrt{\frac{\pi}{2} f_n Q \cdot ASD(f_n)}

Assumptions:

Flat input spectrum near $f_n$
Light damping
SDOF response dominated by resonance

G-RMS from PSD

Overall RMS acceleration computed by integrating the PSD over frequency.

G_{rms} = \sqrt{\int_{f_1}^{f_2} PSD(f) \, df}

Trapezoidal Integration (Log-Log):

G_{rms}^2 = \sum_{i=1}^{n-1} \frac{(f_{i+1} - f_i)(PSD_i + PSD_{i+1})}{2}

For log-log interpolation, use geometric mean approach for more accurate results.

Velocity PSD

PSD_v = \frac{PSD_a}{(2\pi f)^2}

Displacement PSD

PSD_d = \frac{PSD_a}{(2\pi f)^4}

Note: Convert g² to (in/s²)² or (m/s²)² before integrating for velocity/displacement.

Ref: Bendat & Piersol "Random Data" Wiley 2010; Newland "An Introduction to Random Vibrations" Dover 2005

07. Vibration Statistics

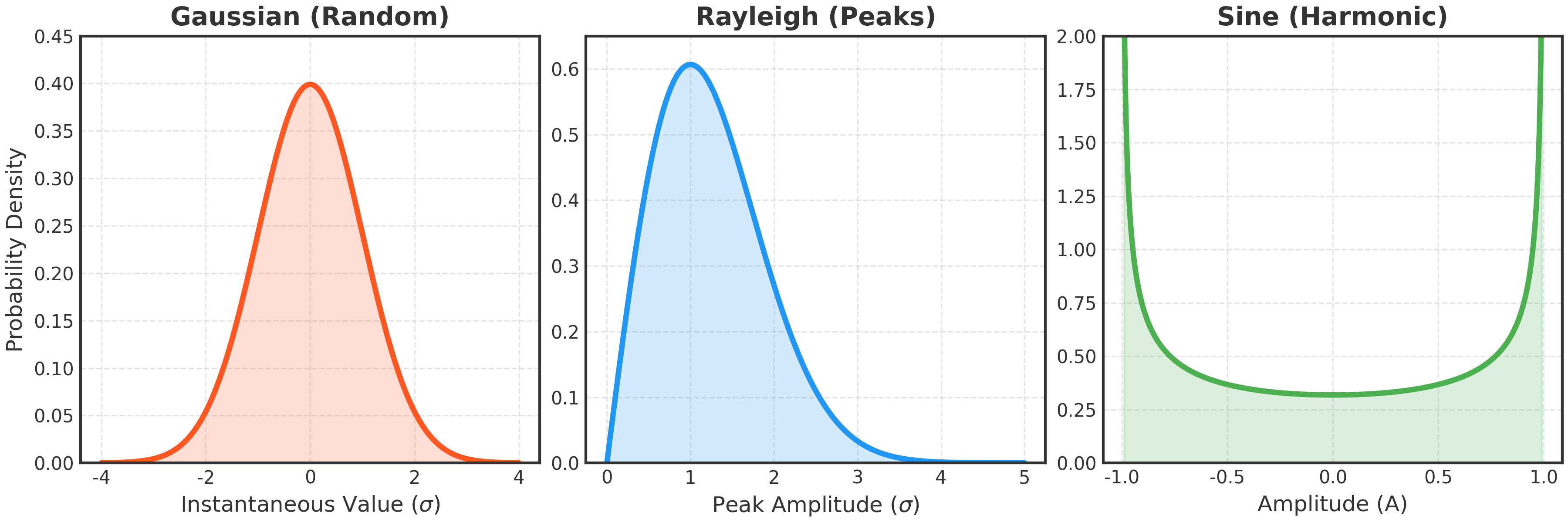
Distributions

Type	Description	Kurtosis
Gaussian	Random vibration instantaneous values.	3.0
Rayleigh	Peak values of narrowband random.	-
Sine	Harmonic vibration ("Bathtub" PDF).	1.5

Sigma ( $\sigma$ ) Peaks

Probability of exceeding $n\sigma$ in Gaussian process:

1 $\sigma$
68.27%
2 $\sigma$
95.45%
3 $\sigma$
99.73%

Ref: Wirsching et al. "Random Vibrations: Theory and Practice" Dover 2006

08. VRS & Extreme Response Spectrum

Vibration Response Spectrum (VRS)

Plot of the RMS response of a series of SDOF oscillators to a random input.

VRS_{rms}(f_n) = \sqrt{\int_0^\infty |H(f, f_n)|^2 \cdot PSD(f) df}

Term	Definition	Units
$VRS_{rms}(f_n)$	RMS response at natural frequency $f_n$	g (or m/s²)
$H(f, f_n)$	SDOF transfer function (DMF)	dimensionless
$PSD(f)$	Input Power Spectral Density	g²/Hz

Extreme Response Spectrum (ERS)

Estimates the maximum expected peak response over a duration $T$ .

ERS(f_n) = \sigma_{rms}(f_n) \cdot \sqrt{2 \ln(\nu_0 T)}

$\sigma_{rms}$ = RMS Response (from VRS)
$\nu_0 \approx f_n$ = Zero-crossing rate
$T$ = Exposure duration (seconds)

Role of Sigma: The term

\sqrt{2 \ln(\nu_0 T)}

represents the "Peak Factor" (number of sigmas). As time

T

increases, the probability of seeing a higher sigma peak increases.

Ref: Irvine "VRS and ERS" vibrationdata.com 2012; Lalanne "Mechanical Vibration and Shock Analysis Vol. 3" Wiley 2014

09. Acoustic Source Models & Correlation

Correlation Visualizer FSP Tool

Acoustic Sources

Type	Description	Use Case
Monopole	Pulsating sphere, omnidirectional.	Low freq exhaust, small components.
Dipole	Two out-of-phase monopoles.	Fan noise, flow separation.
Plane Wave	Uniform wavefront, single direction.	Far-field sources, wind tunnels.
Diffuse Field	Random incidence, uniform energy.	Reverberant chambers, launch bays.

What is Spatial Correlation?

Spatial correlation describes how pressure fluctuations at two points relate to each other. A correlation of 1 means perfectly in-phase (coherent), 0 means uncorrelated (random phase). Why it matters: Correlated pressures add constructively, producing higher structural response than uncorrelated pressures of the same magnitude. Accurate correlation modeling is critical for predicting vibration response to distributed acoustic and aerodynamic loads.

Turbulent Boundary Layer (TBL)

Fluctuating pressure on surface due to flow.

\Phi_{pp}(\omega) \approx \frac{q^2 \delta^*}{U_\infty} \cdot F(\omega \delta^*/U_\infty)

$q$ = Dynamic Pressure
$\delta^*$ = Displacement Thickness
Used for: Aircraft fuselage, fairings, high-speed trains.

TBL Correlation: Corcos Model

Spatial correlation of TBL pressure fluctuations:

\Gamma(\xi, \eta, \omega) = e^{-|\xi|/L_x} e^{-|\eta|/L_y} e^{-i\omega\xi/U_c}

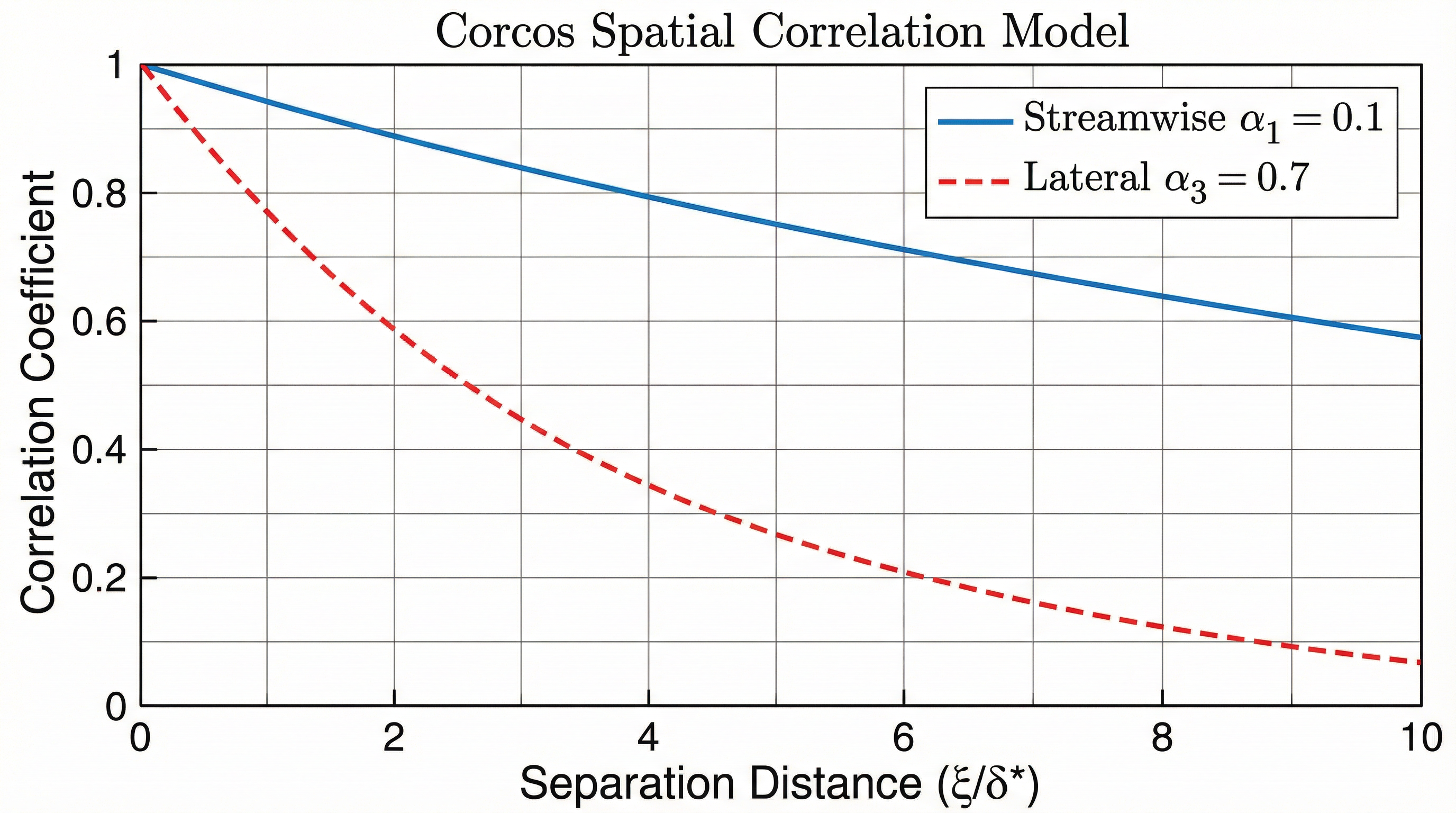
$\xi, \eta$ = Streamwise, spanwise separation
$L_x = U_c / \alpha_x \omega$ , $L_y = U_c / \alpha_y \omega$ (correlation lengths)
$\alpha_x \approx 0.1$ , $\alpha_y \approx 0.7$ (Corcos constants)
$U_c \approx 0.6-0.8 U_\infty$ (convection velocity)

Physical interpretation: TBL correlation decays exponentially with separation distance. Correlation length decreases with frequency (high-freq eddies are smaller). Streamwise correlation is higher than spanwise due to convecting turbulent structures. The phase term $e^{-i\omega\xi/U_c}$ captures the convection of pressure patterns downstream.

Diffuse Acoustic Field (DAF)

Uniform acoustic energy arriving from all directions with random phase.

p_{rms}^2 = \frac{4 W \rho c}{A}

$W$ = Source Power (W)
$A$ = Total Absorption (m² Sabins)

DAF Spatial Correlation

Correlation between two points in a diffuse acoustic field:

\Gamma(r) = \frac{\sin(kr)}{kr}

$r$ = Separation distance between points
$k = \omega/c = 2\pi f/c$ = Acoustic wavenumber
$\Gamma(0) = 1$ (perfect correlation at same point)
First zero at $r = \lambda/2$ (half wavelength)

Physical interpretation: DAF correlation follows a sinc function, oscillating and decaying with distance. Unlike TBL, DAF has no preferred direction—correlation depends only on separation distance, not orientation. Points separated by half a wavelength are uncorrelated. At low frequencies (large λ), correlation extends over larger areas, causing more efficient structural excitation.

Correlation Comparison

Property	TBL (Corcos)	DAF
Decay Shape	Exponential	Sinc (oscillating)
Directional?	Yes (anisotropic)	No (isotropic)
Convection	Yes (phase shift)	No
Corr. Length	$\propto 1/\omega$	$\propto \lambda$

Ref: Corcos "Resolution of Pressure in Turbulence" JASA 1963; Blake "Mechanics of Flow-Induced Sound and Vibration" Academic Press 2017; Fahy "Sound and Structural Vibration" 2007; ESI VA One User Guide

10. Room Acoustics

Reverberation Time (T60)

Time for sound to decay by 60 dB.

T_{60} = \frac{0.161 V}{A} \text{ (Sabine Formula)}

$V$ = Room Volume ( $m^3$ )
$A$ = Total Absorption ( $m^2$ Sabins)

Absorption & Room Constant

A = \sum S_i \alpha_i

R = \frac{A}{1-\bar{\alpha}}

$\alpha$ = Absorption Coeff (0=Reflective, 1=Absorptive)

Schroeder Frequency

f_s = 2000\sqrt{T_{60}/V}

Transition from modal to diffuse field behavior.

Critical Distance

d_c \approx 0.14\sqrt{R}

Distance where direct = reverberant field.

Ref: Kuttruff "Room Acoustics" CRC Press 2016; Long "Architectural Acoustics" Academic Press 2014

11. Statistical Energy Analysis (SEA)

High-frequency energy flow method for complex coupled systems.

Power Balance Equation

\Pi_{in,i} = \omega \eta_i E_i + \sum_{j \neq i} \omega \eta_{ij} n_i \left( \frac{E_i}{n_i} - \frac{E_j}{n_j} \right)

$\Pi_{in}$ = Input Power
$\eta_i$ = Damping Loss Factor
$\eta_{ij}$ = Coupling Loss Factor
$n_i$ = Modal Density
$E_i$ = Total Energy

Subsystems

Plates (Bending, In-plane)
Shells (Cylindrical)
Acoustic Cavities
Beams

Junctions

Point (Beam-Beam)
Line (Plate-Plate)
Area (Plate-Cavity)

Key Concept: Energy flows from high modal energy density to low modal energy density.

Ref: Lyon & DeJong "Theory and Application of SEA" Butterworth 1995; Craik "Sound Transmission Through Buildings" Gower 1996

12. FEA & NASTRAN Dynamics

Solution Sequences (SOL)

SOL	Description	Use Case
103	Normal Modes	Natural Freqs ( $f_n$ ), Mode Shapes
108	Direct Freq. Resp.	Exact solution, freq dependent damping
111	Modal Freq. Resp.	Efficient for large models (uses modes)
112	Modal Transient	Time domain shock (uses modes)

DOF Sets (Matrix Reduction)

A-Set (Analysis)
Retained DOFs for solution. Contains boundary (R) and dynamic (L) DOFs.

O-Set (Omitted)
DOFs reduced out via Guyan reduction (static condensation).

R-Set (Reaction)
Constrained/Boundary DOFs (SPC).

M-Set (Multi-point)
Dependent DOFs defined by MPCs or RBEs.

[M_{aa}]\{\ddot{u}_a\} + [K_{aa}]\{u_a\} = \{F_a\}

Ref: MSC Nastran Dynamic Analysis User's Guide; Cook et al. "Concepts and Applications of Finite Element Analysis" Wiley 2001

13. FEA Mesh Guidelines

Mesh Calculator

Elements per Wavelength

Element Type	Min Elements/λ	Recommended
Linear (4-node quad)	6	8-10
Quadratic (8-node quad)	3	4-6

Rule of Thumb: Element size

L_e \leq \lambda_{min} / N

where N = 6-10 for linear, 3-4 for quadratic elements.

Wave Types & Speeds

Wave Type	Speed Equation	Dispersive?
Longitudinal	$c_L = \sqrt{E/\rho}$	No
Shear	$c_S = \sqrt{G/\rho}$	No
Bending	$c_B = \sqrt[4]{EI\omega^2/(\rho A)}$	Yes
Rayleigh	$c_R \approx 0.92 c_S$	No
Torsional*	$c_T = \sqrt{G/\rho}$	No*

*Torsional waves are dispersive for non-circular cross-sections due to warping effects.

Critical Bending Wavelength

Bending waves are dispersive (speed varies with frequency). At max frequency:

\lambda_B = 2\pi \sqrt[4]{\frac{EI}{\rho A \omega_{max}^2}}

For plates: $\lambda_B = 2\pi \sqrt[4]{\frac{D}{\rho h \omega_{max}^2}}$ where $D = \frac{Eh^3}{12(1-\nu^2)}$

Ref: Langer et al. "More Than Six Elements Per Wavelength" J. Comput. Acoust. 2017; Petyt "Introduction to Finite Element Vibration Analysis" Cambridge 2010

14. DSP & Data Acquisition

Sampling & Aliasing

f_s > 2 f_{max} \text{ (Nyquist Criterion)}

Frequencies above $f_s/2$ fold back (alias) into the baseband.

Dynamic Range & Bit Depth

SNR_{dB} \approx 6.02N + 1.76

$N$ = Number of Bits
16-bit $\approx$ 96 dB
24-bit $\approx$ 144 dB

Window Functions

Window	Use Case	Trade-off
Hanning	Random Vib / General	Good amplitude, fair freq
Flat Top	Calibration / Sine	Best amplitude, poor freq
Rectangular	Transients / Impact	Best freq, leakage risk

Ref: Oppenheim & Schafer "Discrete-Time Signal Processing" Pearson 2009; Harris "On the Use of Windows for Harmonic Analysis" Proc. IEEE 1978

15. Vibroacoustics Scaling Techniques

Scaling Tool

Franken Method

Empirical method for estimating vibration from acoustic excitation.

G_{rms} = 10^{(Y/20)} \text{ g}

Where Y is read from Franken curve at $X = f \cdot L$ (Hz·ft)

Barrett Scaling

Scales reference PSD to new dynamic pressure conditions.

PSD_{new} = PSD_{ref} \cdot \left(\frac{q_{new}}{q_{ref}}\right)^2

$q = \frac{1}{2}\rho V^2$ = Dynamic pressure

Q-Scaling (SPL)

SPL_{new} = SPL_{ref} + 20\log_{10}\left(\frac{q_{new}}{q_{ref}}\right)

Ref: NASA/TM-2009-215902; Franken "Sound-Induced Vibrations" JASA 1962; Laganelli & Howe "Prediction of Pressure Fluctuations" AIAA 1977

16. Sensor Selection Guide

Accelerometer Types

Type	Pros	Cons	Application
IEPE / ICP	Low noise, easy cabling, built-in amp.	Temp limit (~120°C), fixed gain.	General modal, lab testing.
Charge	High temp (> 500°C), rugged.	Requires charge amp, noise sensitive cable.	Turbines, engines, shock.
MEMS (DC)	Measures DC (gravity), cheap.	Higher noise floor, limited bandwidth.	Automotive, tilt, low freq.

Selection Criteria

Sensitivity: 100 mV/g (General) vs 10 mV/g (Shock/High G).
Range: Max G = 5V / Sensitivity. Ensure $G_{peak} < G_{range}$ .
Frequency: Check $\pm 5\%$ response range. Resonance $> 5 \times f_{max}$ .
Mass Loading: Sensor mass $< 0.1 \times$ test object mass.

Ref: PCB Piezotronics "Introduction to Piezoelectric Accelerometers"; Brüel & Kjær "Measuring Vibration" Technical Review

17. Structural Engineering Fundamentals

Beam Calculator

Static Equilibrium

For a body in equilibrium, the sum of all forces and moments must be zero:

\sum \vec{F} = 0 \quad \text{and} \quad \sum \vec{M} = 0

2D (Planar)

\sum F_x = 0

\sum F_y = 0

\sum M_z = 0

3D (Spatial)

\sum F_x = \sum F_y = \sum F_z = 0

\sum M_x = \sum M_y = \sum M_z = 0

Free Body Diagram (FBD) Checklist

Isolate the body of interest
Show all external forces (applied loads, reactions)
Include weight at center of gravity
Replace supports with reaction forces
Define positive sign conventions

Support Reactions

Support Type	Reactions Provided	DOF Constrained
Roller	1 force (⊥ to surface)	1
Pin/Hinge	2 forces (Fx, Fy)	2
Fixed/Cantilever	2 forces + 1 moment	3

Internal Forces

Axial (N)
Tension/Compression

Shear (V)
Transverse force

Moment (M)
Bending

Ref: Hibbeler "Structural Analysis" Pearson 2017; Gere & Goodno "Mechanics of Materials" Cengage 2018

18. Cylinders, Rings, Shells & Cones

Ring Frequency

Frequency at which circumferential wavelength equals the circumference (breathing mode):

f_r = \frac{c_L}{\pi d} = \frac{1}{\pi d}\sqrt{\frac{E}{\rho}}

$c_L$ = Longitudinal wave speed in shell material
$d$ = Shell diameter

Critical (Coincidence) Frequency

Frequency where bending wavelength in shell equals acoustic wavelength:

f_{cr} \approx \frac{c^2}{1.8 \cdot c_L \cdot h}

$c$ = Speed of sound in fluid (air ≈ 343 m/s)
$h$ = Shell wall thickness

Shell Behavior Regimes

Frequency Range	Behavior	Dominant Mode
$\Omega < 0.77 h/a$	Beam-like	n = 1 (bending)
$0.77 h/a < \Omega < 0.6$	Shell modes	n = 2, 3, 4... (lobar)
$\Omega > 0.6$	Plate-like	High-order modes

Where $\Omega = \omega a / c_L$ is the non-dimensional frequency parameter.

Circumferential Mode Shapes

n = 0
Breathing

n = 1
Beam

n = 2
Ovaling

n ≥ 3
Lobar

Radiation Efficiency

\sigma = \frac{W_{rad}}{\rho c S \langle v^2 \rangle}

Frequency	σ Behavior	Notes
$f < f_{cr}$	$\sigma \ll 1$	Poor radiator (subsonic bending waves)
$f \approx f_r$	$\sigma \approx 1$	Ring frequency peak
$f \approx f_{cr}$	$\sigma \gg 1$	Coincidence peak
$f > f_{cr}$	$\sigma \rightarrow 1$	Efficient radiator

Ring Stiffener Effects

Adding ring stiffeners shifts natural frequencies:

f_{stiffened} \approx f_{unstiffened} \sqrt{1 + \frac{EI_{ring}}{EI_{shell} \cdot L_s}}

$L_s$ = Stiffener spacing
Creates pass bands and stop bands in frequency response
Stop bands occur near stiffener resonances

Ref: Hambric "Structural Acoustics Tutorial" Inter-noise 2022; Irvine "Shell Vibration" vibrationdata.com 2008; Maidanik "Response of Ribbed Panels" JASA 1962; Cremer/Heckl "Structure-Borne Sound" Springer 2005

19. Aerospace Material Properties

Common Aerospace Materials (Metric)

Material	E (GPa)	ρ (kg/m³)	G (GPa)	ν
Al 6061-T6	68.9	2700	26.0	0.33
Al 7075-T6	71.7	2810	26.9	0.33
Ti-6Al-4V	113.8	4430	44.0	0.34
Steel 4340	205	7850	80.0	0.29
Inconel 718	200	8190	77.0	0.30
CFRP (Quasi)	70	1600	5.0	0.30
Mg AZ31B	45	1770	17.0	0.35

Common Aerospace Materials (English)

Material	E (Msi)	ρ (lb/in³)	G (Msi)
Al 6061-T6	10.0	0.098	3.77
Al 7075-T6	10.4	0.102	3.90
Ti-6Al-4V	16.5	0.160	6.38
Steel 4340	29.7	0.284	11.6
Inconel 718	29.0	0.296	11.2
CFRP (Quasi)	10.2	0.058	0.73
Mg AZ31B	6.5	0.064	2.47

Wave Speeds:

c_L = \sqrt{E/\rho}

c_S = \sqrt{G/\rho}

. Higher E/ρ ratio = faster wave propagation = larger mesh elements allowed.

Ref: MIL-HDBK-5J / MMPDS-01; ASM Handbook Vol. 2 "Properties and Selection: Nonferrous Alloys"

20. Rotating Dynamics

Campbell Diagram

Plot of natural frequencies vs. rotational speed, showing critical speed intersections.

Component	Description
Mode Lines	Natural frequencies that may vary with speed due to stiffening
Excitation Lines	1X, 2X, nX lines representing synchronous excitation
Critical Speeds	Intersections where excitation frequency = natural frequency
Operating Range	Shaded region showing normal operating speed range

Blade Mode Stiffening

Centrifugal forces increase blade stiffness with rotational speed:

\omega_n(\Omega) = \sqrt{\omega_0^2 + k \cdot \Omega^2}

$\omega_0$ = Natural frequency at rest (Ω = 0)
$k$ = Stiffening coefficient (mode-dependent)
$\Omega$ = Rotational speed (rad/s)

Excitation Lines

Line	Frequency	Typical Source
1X	$f = \Omega/(2\pi)$	Unbalance, misalignment
2X	$f = 2\Omega/(2\pi)$	Misalignment, looseness
nX	$f = n\Omega/(2\pi)$	Blade pass (n = blade count)
Non-integer	Various	Subsynchronous whirl, instabilities

Example Campbell Diagram

Mode parameters: Mode 1 (f₀=40 Hz, k=0.0001), Mode 2 (f₀=100 Hz, k=0.00005), Mode 3 (f₀=180 Hz, k=0.00002).
Critical speeds: Mode 1 × 1X at 2800 RPM (47 Hz), Mode 2 × 1X at 7000 RPM (117 Hz) - within operating range!

Resonance Condition

n \cdot \Omega_{crit} = \omega_n(\Omega_{crit})

Solve for critical speed $\Omega_{crit}$ where excitation line (nX) intersects mode line.

Engineering Review Checklist

Identify all critical speeds within operating range
Ensure adequate separation margin (typically 15-20%)
Check for subsynchronous instabilities
Verify damping at critical speeds
Consider transient operation through critical speeds
Evaluate blade pass frequency interactions
Account for temperature effects on material properties

Shaft Speed to Frequency:

f_{Hz} = \frac{\Omega_{RPM}}{60}

Blade Pass Frequency:

f_{BP} = n_{blades} \cdot \frac{\Omega_{RPM}}{60}

Design Guidance: API 617 (compressors) requires critical speeds to be at least 15% away from operating speed range. For transient operation, ensure adequate damping or rapid acceleration through critical speeds.

Ref: API 617 "Axial and Centrifugal Compressors"; Childs, "Turbomachinery Rotordynamics" Wiley 1993; Vance, "Rotordynamics of Turbomachinery" Wiley 1988

21. PSD Calculation from Time History

Welch's Method Overview

Standard approach for estimating PSD from sampled time data using averaged periodograms.

Preprocess: Remove mean, apply detrending, filter if needed
Segment: Divide time history into overlapping frames (typ. 50% overlap)
Window: Apply window function (e.g., Hanning) to each segment
FFT: Compute FFT for each windowed segment: $X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-j2\pi kn/N}$
Power: Calculate |X_k|² for each segment
Average: Average the power spectra across all segments
Scale to PSD: Convert to single-sided PSD with window energy correction:
$S_{xx}(f_k) = \frac{2 \cdot C_E^2 \cdot |X_k|^2}{f_s \cdot N}$
where C_E = window energy correction factor (see table below), f_s = sample rate, N = FFT length. Factor of 2 converts to single-sided (positive frequencies only). For Hanning window, C_E = 1.63.

Key Parameters

Parameter	Formula	Notes
Frequency Resolution	$\Delta f = \frac{1}{T} = \frac{f_s}{N}$	T = segment duration, N = samples/segment
Segment Duration	$T = \frac{N}{f_s}$	Longer T → finer Δf but fewer averages
Nyquist Frequency	$f_{max} = \frac{f_s}{2}$	Maximum resolvable frequency
N for desired Δf	$N = \frac{f_s}{\Delta f}$	Must be power of 2 for efficient FFT

Example: For f_s = 4000 Hz and desired Δf = 5 Hz:

N = \frac{4000}{5} = 800 \text{ samples}

→ Use N = 1024 (next power of 2) → actual Δf = 3.9 Hz

Segment duration T = 1024/4000 = 0.256 seconds

Time vs. Frequency Resolution Trade-off

Fundamental trade-off: finer frequency resolution requires longer segments, reducing time resolution and number of averages.

\Delta f \cdot T = 1

The uncertainty principle: cannot have arbitrarily fine resolution in both domains simultaneously.

Δf	Segment T	Pros	Cons
1 Hz	1.0 sec	Fine frequency detail, resolves closely-spaced peaks	Fewer averages, higher variance, poor for short events
5 Hz	0.2 sec	Good balance for most applications	May not resolve narrow-band features
25 Hz	0.04 sec	Many averages, low variance, captures transients	Smears frequency content, poor peak resolution

SMC-S-016 Flight Data Processing

Per SMC-S-016 "Test Requirements for Launch, Upper-Stage, and Space Vehicles":

Segment Duration: "Use 1-second time segments" for computing PSDs from flight data
Overlap: "50% overlap between adjacent segments" to maximize statistical DOF
Bandwidth: 5 Hz constant bandwidth with conversion to 1/6th octave bands for final presentation (no need to go narrower than 5 Hz at low frequencies)
Window: Hanning window recommended to reduce spectral leakage

Window Functions

Windows reduce spectral leakage from discontinuities at segment boundaries. Each window trades off main lobe width vs. side lobe suppression.

Window	Amp. Corr.	Energy Corr.	ENBW	Use Case
Rectangular	1.00	1.00	1.00	Transients (full capture)
Hanning	2.00	1.63	1.50	Random vibration (most common)
Hamming	1.85	1.59	1.36	General purpose
Blackman	2.80	1.97	1.73	Low leakage required
Flat Top	4.18	2.26	3.77	Amplitude accuracy (calibration)

ENBW = Equivalent Noise Bandwidth (in frequency bins). For PSD, apply energy correction.

Overlap & Degrees of Freedom

Overlap reuses data between segments, increasing effective DOF for the same total duration.

Overlap	DOF per Frame	Efficiency	Notes
0%	2.00	100%	No data reuse
50%	~1.85	~185%	Optimal for Hanning window
75%	~1.20	~240%	Diminishing returns

DOF Formula:

n_{DOF} \approx 2 \cdot n_{avg} \cdot \eta_{overlap}

where n_avg = number of averaged segments, η_overlap = overlap efficiency factor

Time for N DOF (50% overlap, Hanning):

t_{total} \approx \frac{n_{DOF}}{2 \cdot 1.85} \cdot T = 0.27 \cdot n_{DOF} \cdot T

Higher DOF = lower variance = smoother PSD estimate

PSD Confidence Intervals

PSD estimates follow chi-squared distribution with n_DOF degrees of freedom.

\frac{n_{DOF} \cdot \hat{S}(f)}{\chi^2_{\alpha/2, n_{DOF}}} \leq S(f) \leq \frac{n_{DOF} \cdot \hat{S}(f)}{\chi^2_{1-\alpha/2, n_{DOF}}}

DOF	90% CI (dB)	95% CI (dB)
10	±2.6	±3.2
50	±1.1	±1.3
100	±0.8	±0.9
200	±0.5	±0.6

Preprocessing & Filtering

Mean Removal	Subtract DC offset to prevent low-frequency bias. Critical before windowing as DC leaks into adjacent bins.
Detrending	Remove linear/polynomial trends from sensor drift. Use least-squares fit for polynomial order 1-3.
Anti-Alias Filter	Applied during acquisition. Cutoff f_c = 0.4–0.45 × f_s typical. Use steep rolloff (8th order Butterworth or better) to ensure >80 dB attenuation at Nyquist.
Highpass Filter	Remove content below analysis band. Set cutoff at 0.5–1× lowest frequency of interest. Use 4th order Butterworth (24 dB/octave) minimum.

Anti-Aliasing Filter Selection

Rule of thumb: f_c = 0.4 × f_s provides margin for filter rolloff.

Sample Rate (f_s)	Recommended Cutoff	Usable Bandwidth
1,000 Hz	400 Hz	5–400 Hz
4,000 Hz	1,600 Hz	5–1,600 Hz
10,000 Hz	4,000 Hz	5–4,000 Hz
50,000 Hz	20,000 Hz	5–20,000 Hz

Higher order filters allow cutoff closer to Nyquist but introduce phase distortion. For shock/transient data, use linear-phase (FIR) filters.

DC & Low-Frequency Handling

DC Offset: Always remove mean before FFT. Even small DC offsets create large low-frequency artifacts due to spectral leakage.
Sensor Drift: Accelerometers exhibit 1/f noise below ~5 Hz. Apply highpass filter or discard bins below analysis band.
Integration Effects: When integrating acceleration to velocity/displacement, DC and low-frequency errors accumulate. Highpass filter before integration.
Recommended Practice: Set analysis lower bound at 5–10 Hz for typical accelerometer data unless sensor is specifically rated for lower frequencies.

Key Insight: The choice of segment length is the primary trade-off. Longer segments give finer frequency resolution but fewer averages (higher variance). For stationary signals, use longer segments. For non-stationary or transient data, use shorter segments to capture time-varying behavior.

Ref: Bendat & Piersol "Random Data" Wiley 2010; SMC-S-016 (2014) "Test Requirements for Launch Vehicles" Section 6.2.3; Welch "The Use of FFT for Estimation of Power Spectra" IEEE 1967; Harris "On the Use of Windows" Proc. IEEE 1978

22. SRS CALCULATION FROM TIME HISTORY

SRS Calculator Pyroshock Tool

What is a Shock Response Spectrum?

The Shock Response Spectrum (SRS) characterizes a transient's potential to excite resonant structures. It plots the peak response of an array of single degree-of-freedom (SDOF) oscillators, each with a different natural frequency but the same damping ratio, when subjected to the same base excitation.

Key concept: The SRS does not contain all information about the original time history—many different transients can produce the same SRS. It captures only the peak instantaneous responses at each frequency.

Smallwood Ramp Invariant Algorithm

The most widely used SRS calculation method is the ramp invariant digital recursive filter developed by David O. Smallwood (1981). This method connects impulse-response samples with straight lines to reduce aliasing errors.

Algorithm Steps:

Define Parameters: Set damping ratio ξ (typically 5%, Q=10) and analysis frequencies
Design Filter: For each natural frequency f_n, compute ramp invariant filter coefficients
Apply Filter: Process the acceleration time history through each SDOF digital filter
Extract Peaks: Record maximum positive, negative, and absolute (maximax) responses
Build Spectrum: Plot peak response vs. natural frequency on log-log axes

SDOF Response Equation

Each oscillator in the SRS bank follows the equation of motion:

\ddot{z} + 2\zeta\omega_n\dot{z} + \omega_n^2 z = -\ddot{x}_{base}

where z = relative displacement, ω_n = 2πf_n, ζ = damping ratio, and ẍ_base = input acceleration.

Absolute Acceleration Response:

\ddot{x}_{response} = \ddot{x}_{base} + \ddot{z} = -2\zeta\omega_n\dot{z} - \omega_n^2 z

Why Absolute Acceleration?

The SRS plots absolute acceleration because it directly relates to the forces experienced by internal components. For a component of mass m mounted on a resonant structure, the force is F = m·ẍ_absolute. Relative displacement z is useful for clearance/sway space analysis, but absolute acceleration determines whether components survive the shock. This is why shock test specifications are written in terms of acceleration SRS—they define the maximum forces that equipment must withstand.

Q Factor & Damping

The quality factor Q defines the sharpness of resonance and is related to damping ratio:

Q = \frac{1}{2\zeta}

Q Factor	Damping ζ	Application
Q = 10	5%	Standard for pyrotechnic shock (ISO 18431-4, MIL-STD-810)
Q = 25	2%	Lightly damped structures, conservative analysis
Q = 50	1%	Very lightly damped, electronic components
Q = 5	10%	Heavily damped systems, transportation shock

Higher Q = sharper peaks, more conservative SRS. An SRS plot is incomplete without specifying Q.

SRS Types

Type	Definition	Use Case
Maximax	max(\|positive\|, \|negative\|) over entire duration	Most common, conservative envelope
Primary	Peak response during shock application	Forced response analysis
Residual	Peak response after shock ends (free vibration)	Ringing/settling analysis
Positive	Maximum positive response	Tensile stress analysis
Negative	Maximum negative response	Compressive stress analysis

Frequency Spacing

SRS frequencies are logarithmically spaced in fractional octave bands:

f_{k+1} = f_k \cdot 2^{1/n}

where n = points per octave (e.g., n=6 for 1/6 octave spacing)

Spacing	Points/Octave	Ratio	Application
1/1 Octave	1	2.000	Coarse overview
1/3 Octave	3	1.260	General analysis
1/6 Octave	6	1.122	Standard (ISO 18431-4)
1/12 Octave	12	1.059	Fine resolution
1/24 Octave	24	1.029	High resolution

Selection Guidance: Choose spacing so that the frequency increment is smaller than the half-power bandwidth of the SDOF filter: Δf < f_n/Q. For Q=10, 1/6 octave (12.2% spacing) satisfies this for all frequencies.

Sample Rate Requirements

The input time history must be sampled fast enough to accurately capture the shock and compute responses at high frequencies:

Minimum: f_s ≥ 10 × f_max (highest SRS frequency)
Recommended: f_s ≥ 20 × f_max for accurate peak capture
Example: For SRS to 10 kHz, sample at ≥100 kHz (preferably 200 kHz)

Max SRS Freq	Min Sample Rate	Recommended	Application
2 kHz	20 kHz	40 kHz	Transportation shock
10 kHz	100 kHz	200 kHz	Pyrotechnic shock
100 kHz	1 MHz	2 MHz	Near-field pyroshock

Compensation for Insufficient Sample Rate:

When the sample rate is less than 10× the highest analysis frequency, the digital filter underestimates the true peak response. A correction factor can be applied:

C_{sr} = \frac{1}{\text{sinc}(\pi f_n / f_s)} = \frac{\pi f_n / f_s}{\sin(\pi f_n / f_s)}

f_s/f_n Ratio	Correction C_sr	Error if Uncorrected
20	1.004	-0.4%
10	1.017	-1.7%
8	1.026	-2.6%
5	1.067	-6.3%
4	1.111	-10%
3	1.209	-17%

Recommendation: Apply C_sr correction when f_s/f_n < 10. Below ratio of 5, consider resampling/interpolating the time history before SRS calculation for more reliable results. The sinc correction accounts for the averaging effect of discrete sampling on peak values.

Typical Frequency Ranges

Shock Type	Frequency Range	Typical Q
Transportation (drop, handling)	1 Hz – 500 Hz	Q = 5–10
Seismic	0.1 Hz – 100 Hz	Q = 5–10
Pyrotechnic (far-field)	100 Hz – 10 kHz	Q = 10
Pyrotechnic (near-field)	100 Hz – 100 kHz	Q = 10
Ballistic shock	10 Hz – 50 kHz	Q = 10

Velocity & Displacement SRS

SRS can be computed for velocity or displacement by integrating the acceleration response:

Pseudo-Velocity	$V_{pseudo} = \frac{A_{max}}{\omega_n} = \frac{A_{max}}{2\pi f_n}$
Pseudo-Displacement	$D_{pseudo} = \frac{A_{max}}{\omega_n^2} = \frac{A_{max}}{(2\pi f_n)^2}$

Pseudo-velocity SRS is useful for assessing structural stress (σ ∝ velocity). Tripartite plots show all three on one graph.

50 IPS Shock Severity Threshold

The "50 inches per second" (50 IPS) rule is a widely-used empirical threshold for assessing shock severity and potential for damage:

The 50 IPS Rule: When pseudo-velocity exceeds approximately 50 in/s (1.27 m/s), the shock is considered potentially damaging to typical aerospace/military hardware. This threshold corresponds to stress levels approaching yield in many structural materials.

Pseudo-Velocity	Severity	Typical Concern
< 20 IPS	Low	Generally benign for most equipment
20–50 IPS	Moderate	May cause fatigue damage with repeated exposure
50–100 IPS	High	Potential yield stress in structural elements
> 100 IPS	Severe	Likely permanent deformation or failure

Physical Basis: For a simple beam, bending stress σ ∝ strain rate ∝ velocity. The 50 IPS threshold (~100 dB re 10^-6 in/s) empirically correlates with stress levels of 10,000–20,000 psi in aluminum structures, approaching yield for many alloys. This makes pseudo-velocity SRS a direct indicator of damage potential, independent of frequency.

Preprocessing for SRS

Mean Removal	Remove DC offset before processing. DC creates artificial low-frequency content.
Zero Padding	Extend time history with zeros after shock to capture residual response (typically 2× shock duration).
Anti-Alias Filter	Ensure data was acquired with proper anti-aliasing (f_c < 0.4 × f_s).
Integrity Check	Positive and negative SRS should be similar for symmetric pulses. Large asymmetry may indicate clipping or sensor issues.

Key Insight: Unlike PSD which characterizes stationary random vibration, SRS characterizes transient deterministic events. The SRS is a worst-case envelope—it shows the maximum response that could occur at each frequency, regardless of when it occurs during the event.

Ref: Smallwood "An Improved Recursive Formula for Calculating Shock Response Spectra" Shock & Vibration Bulletin No. 51, 1981; ISO 18431-4:2007 "Shock-response spectrum analysis"; Irvine "An Introduction to the Shock Response Spectrum" Vibrationdata 2012; MIL-STD-810G Method 516.6

23. SOUND TRANSMISSION LOSS

TL Calculator

Definition

Sound Transmission Loss (TL or STL) quantifies the reduction in sound power as it passes through a partition:

TL = 10 \log_{10}\left(\frac{W_{incident}}{W_{transmitted}}\right) = 10 \log_{10}\left(\frac{1}{\tau}\right) \text{ dB}

where τ is the transmission coefficient (ratio of transmitted to incident sound power)

Transmission Loss Regions for Isotropic Panels

The TL behavior of a panel varies with frequency, exhibiting four distinct regions:

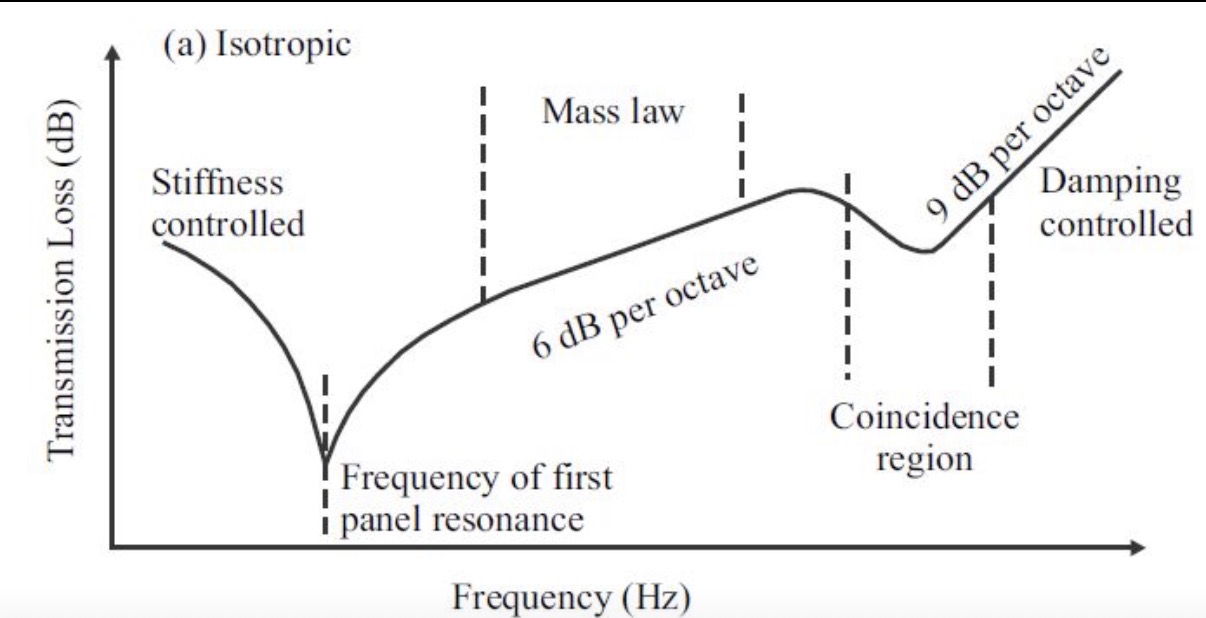
Region	Frequency Range	Controlling Factor	TL Behavior
Stiffness Controlled	f < f₁ (first resonance)	Panel bending stiffness	TL decreases with frequency
Resonance Region	Near f₁	Panel resonances	TL dip at panel modes
Mass Law	f₁ < f < f_c	Panel surface mass	+6 dB per octave
Coincidence Region	f ≈ f_c	Wave matching	TL dip (minimum)
Damping Controlled	f > f_c	Internal damping	+9 dB per octave

Mass Law

In the mass-controlled region, TL depends primarily on surface density and frequency:

TL_{mass} = 20 \log_{10}(m'' f) - 47.3 \text{ dB}

where m'' = surface mass density (kg/m²), f = frequency (Hz)

Mass Law Rules of Thumb:

Doubling mass → +6 dB TL
Doubling frequency → +6 dB TL
Field incidence (random) reduces TL by ~5 dB vs. normal incidence

Critical (Coincidence) Frequency

Coincidence occurs when the acoustic wavelength in air matches the bending wavelength in the panel:

f_c = \frac{c^2}{2\pi} \sqrt{\frac{\rho h}{D}} = \frac{c^2}{2\pi h} \sqrt{\frac{12\rho(1-\nu^2)}{E}}

where c = speed of sound in air (~343 m/s), h = panel thickness, ρ = panel density, D = bending stiffness, E = Young's modulus, ν = Poisson's ratio

Simplified Formula:

f_c \approx \frac{12.6}{h} \sqrt{\frac{\rho}{E}} \text{ Hz (for steel/aluminum, h in mm)}

Material	f_c × h (Hz·mm)	1 mm plate f_c	10 mm plate f_c
Steel	~12,400	12.4 kHz	1.24 kHz
Aluminum	~12,000	12.0 kHz	1.20 kHz
Glass	~12,700	12.7 kHz	1.27 kHz
Plywood	~20,000	20 kHz	2.0 kHz
Gypsum board	~35,000	35 kHz	3.5 kHz

TL at Coincidence

At the critical frequency, TL depends strongly on damping:

TL_{coincidence} = TL_{mass} + 10 \log_{10}(2\eta) \text{ dB}

where η = loss factor. Higher damping reduces the coincidence dip.

Loss Factor η	Coincidence Penalty	Typical Material
0.001	-27 dB	Steel, aluminum
0.01	-17 dB	Glass
0.03	-12 dB	Concrete
0.1	-7 dB	Damped steel
0.3	-2 dB	Heavily damped composite

Above Coincidence (Damping Controlled)

Above the critical frequency, TL increases at approximately 9 dB per octave:

TL = TL_{mass} + 10 \log_{10}\left(\frac{2\eta f}{f_c}\right) \text{ dB, for } f > f_c

The 9 dB/octave slope comes from: 6 dB/octave (mass law) + 3 dB/octave (damping term)

First Panel Resonance

For a simply-supported rectangular panel:

f_{1,1} = \frac{\pi}{2} \sqrt{\frac{D}{\rho h}} \left(\frac{1}{a^2} + \frac{1}{b^2}\right)

where a, b = panel dimensions, D = Eh³/12(1-ν²) = bending stiffness

Design Strategies

Strategy	Effect on TL	Trade-offs
Increase mass	+6 dB per doubling	Weight penalty
Add damping	Reduces coincidence dip	Cost, weight
Double-wall construction	+12 dB/octave above mass-air-mass resonance	Thickness, complexity
Constrained layer damping	Raises TL at/above f_c	Weight, cost
Sandwich construction	Shifts f_c lower, higher stiffness	Complex coincidence behavior

Double-Wall Construction

Double-wall partitions provide significantly higher TL than single walls of equivalent mass by decoupling the two panels with an air gap.

Mass-Air-Mass Resonance

The air gap acts as a spring between the two panel masses, creating a resonance at:

f_0 = \frac{1}{2\pi} \sqrt{\frac{\rho_{air} c^2}{d} \left(\frac{1}{m_1} + \frac{1}{m_2}\right)}

where d = air gap depth, m₁, m₂ = panel surface masses (kg/m²), ρ_air ≈ 1.21 kg/m³, c ≈ 343 m/s

TL Behavior by Frequency Region

Region	Frequency Range	TL Behavior
Below f₀	f < f₀	Follows combined mass law (~6 dB/octave)
At Resonance	f ≈ f₀	TL dip (panels move in phase)
Above f₀	f > f₀	~12 dB/octave (6 dB mass + 6 dB decoupling)

Simplified Double-Wall TL (above f₀)

TL_{double} \approx TL_1 + TL_2 + 20\log_{10}\left(\frac{f}{f_0}\right) \text{ dB}

where TL₁, TL₂ = individual panel mass law TL values

Design Guidelines

Parameter	Effect	Recommendation
Air gap depth	Larger d → lower f₀	Maximize gap (50-100 mm typical)
Panel mass ratio	Dissimilar masses broaden improvement	Use different thicknesses/materials
Cavity absorption	Reduces cavity resonances	Add fiberglass/mineral wool
Structural bridges	Short-circuit decoupling	Minimize rigid connections
Edge sealing	Flanking paths reduce TL	Seal all gaps and penetrations

Example: Two 3 mm aluminum panels (m = 8.1 kg/m² each) with 50 mm air gap: f₀ ≈ 84 Hz. At 1 kHz, double-wall provides ~25 dB more TL than a single 6 mm panel of the same total mass.

Key Insight: For aerospace applications, the coincidence frequency often falls within the critical frequency range (100 Hz – 10 kHz). Designing panels with f_c above the frequency range of interest, or adding sufficient damping to mitigate the coincidence dip, is essential for achieving target TL performance. For maximum TL, consider double-wall construction with the mass-air-mass resonance below the frequency range of interest.

Ref: Fahy & Gardonio "Sound and Structural Vibration" 2nd Ed. Academic Press 2007; Cremer, Heckl & Petersson "Structure-Borne Sound" 3rd Ed. Springer 2005; Beranek & Vér "Noise and Vibration Control Engineering" 2nd Ed. Wiley 2006; ISO 10140 "Acoustics - Laboratory measurement of sound insulation"

24. INSERTION LOSS

IL Calculator

Definition

Insertion Loss (IL) quantifies the reduction in sound pressure level at a receiver location due to the insertion of an acoustic treatment (barrier, enclosure, silencer):

IL = L_{p,before} - L_{p,after} \text{ dB}

where L_p,before = SPL without treatment, L_p,after = SPL with treatment

Barrier Insertion Loss

Sound barriers reduce noise by blocking the direct path and forcing sound to diffract over the top edge.

Fresnel Number

The key parameter for barrier performance is the Fresnel number:

N = \frac{2\delta}{\lambda} = \frac{2\delta f}{c}

where δ = path length difference (A+B-d), λ = wavelength, f = frequency, c = speed of sound

Path Difference Geometry

δ = A + B - d

A = source to barrier top, B = barrier top to receiver, d = direct path (source to receiver)

Maekawa's Empirical Formula

For a thin, rigid barrier with N > 0 (receiver in shadow zone):

IL = 10 \log_{10}(3 + 20N) \text{ dB}

Valid for 0.01 ≤ N ≤ 12.5, point source, no ground reflections

ISO 9613-2 Barrier Formula

More accurate formula accounting for ground and meteorological effects:

IL = 10 \log_{10}\left(3 + \frac{C_2}{\lambda} \cdot C_3 \cdot z \cdot K_{met}\right) \text{ dB}

where z = path difference, C₂ = 20 (single diffraction), C₃ = 1 for single edge, K_met = meteorological correction

Fresnel Number N	IL (Maekawa)	Typical Application
0.01	5 dB	Grazing incidence
0.1	8 dB	Low barrier
1.0	13 dB	Moderate barrier
10	23 dB	High barrier, high frequency
100	33 dB	Very effective barrier

Enclosure Insertion Loss

Acoustic enclosures surround a noise source to contain radiated sound.

Ideal Enclosure (No Leaks)

IL = TL + 10 \log_{10}\left(\frac{S_{enclosure}}{R}\right) \text{ dB}

where TL = transmission loss of enclosure walls, S = enclosure surface area, R = room constant of interior

Simplified Enclosure IL

For enclosures with internal absorption:

IL \approx TL - 10 \log_{10}\left(1 + \frac{S(1-\bar{\alpha})}{\bar{\alpha} S}\right) \text{ dB}

where ᾱ = average absorption coefficient inside enclosure

Enclosure Type	Typical IL	Notes
Light sheet metal (no absorption)	10-15 dB	Limited by internal reverb
Sheet metal + internal lining	15-25 dB	2" fiberglass typical
Double-wall with absorption	25-40 dB	High-performance
Lead-lined/composite	35-50 dB	Critical applications

Silencer/Muffler Insertion Loss

Silencers attenuate sound in ducts and exhaust systems through reactive and dissipative mechanisms.

Dissipative Silencer (Lined Duct)

Attenuation per unit length for rectangular duct with absorptive lining:

IL = 1.05 \cdot \frac{\alpha^{1.4} \cdot P}{S^{0.5}} \cdot L \text{ dB}

where α = absorption coefficient, P = lined perimeter, S = open area, L = length

Reactive Silencer (Expansion Chamber)

Simple expansion chamber transmission loss:

TL = 10 \log_{10}\left[1 + \frac{1}{4}\left(m - \frac{1}{m}\right)^2 \sin^2(kL)\right] \text{ dB}

where m = S₂/S₁ = expansion ratio, k = 2πf/c = wavenumber, L = chamber length

Silencer Type	Mechanism	Typical IL	Best For
Lined duct	Dissipative	3-10 dB/m	Mid-high frequency
Expansion chamber	Reactive	5-25 dB (tuned)	Low frequency tones
Helmholtz resonator	Reactive	10-30 dB (narrow band)	Specific frequencies
Combination	Both	15-40 dB	Broadband + tones

Design Guidelines

Treatment	Key Design Factor	Common Pitfall
Barriers	Maximize path difference δ	Flanking paths around ends
Enclosures	Seal all gaps, add internal absorption	Leaks dominate at high TL
Silencers	Match to frequency content	Flow noise regeneration

Key Insight: Insertion loss is always measured or predicted for a specific source-receiver geometry. Unlike TL (a material property), IL depends on the entire acoustic path including reflections, flanking, and source directivity. Always verify predicted IL with field measurements when possible.

Ref: Maekawa, Z. "Noise Reduction by Screens" Applied Acoustics 1968; ISO 9613-2 "Acoustics - Attenuation of sound during propagation outdoors"; Beranek & Vér "Noise and Vibration Control Engineering" 2nd Ed. Wiley 2006; Bies & Hansen "Engineering Noise Control" 5th Ed. CRC Press 2017

25. FEA Best Practices for Dynamic Analysis

Guidance for building FE models from CAD for modal and modal transient analysis.

Element Type Selection

Structure Type	Recommended Element	Notes
Thin-walled (t/L < 0.1)	CQUAD4, CTRIA3	Shell elements capture bending efficiently
Thick structures	CHEXA, CPENTA	Use when t/L > 0.1 or 3D stress needed
Slender members	CBAR, CBEAM	L/d > 10; include shear deformation for short beams
Stiffeners on panels	CBEAM on shell	Offset to mid-plane; check eccentricity
Fastener patterns	CBUSH, CFAST	Avoid over-stiffening with RBE2

Linear vs. Quadratic: Linear elements (CQUAD4) are preferred for dynamics—faster solve, adequate accuracy with proper mesh density. Quadratic (CQUAD8) needed only for curved geometry or stress accuracy.

Composite Modeling

Card	Use Case	Key Inputs
PCOMP	Standard layup	MIDi, Ti, THETAi per ply; Z0 offset
PCOMPG	Global ply IDs	Same as PCOMP + global ply tracking
MAT8	Orthotropic 2D	E1, E2, G12, NU12, RHO

Define fiber direction (0°) consistently—typically along primary load path
Use symmetric layups to avoid bend-twist coupling artifacts
For equivalent smeared properties: use [A], [B], [D] matrices from CLT

Joint Modeling

Joint Type	Modeling Approach	Stiffness Guidance
Bolted (stiff)	RBE2 or CBUSH	K ≈ E·A/L for axial; include preload effects
Bolted (flexible)	CBUSH with K, B	Huth/Swift formula for shear flexibility
Bonded	Tied contact or RBE2	Assume rigid unless adhesive layer modeled
Spot welds	CWELD, CFAST	Diameter-based stiffness; check nugget size
Interference fit	CBUSH radial	K = p·π·d·L/δ (pressure-based)

RBE2 (Rigid): All dependent DOFs slaved to independent node. Over-stiffens locally—use sparingly.

RBE3 (Interpolation): Distributes loads/motion. Does NOT add stiffness. Good for load application.

Damping Specification

Method	Card/Field	When to Use
Modal (ζ)	TABDMP1	Frequency-dependent ζ; most common for modal FRF
Structural (G)	GE on MAT1, PARAM G	Constant loss factor η = 2ζ; hysteretic
Viscous (B)	CBUSH, CDAMP	Discrete dashpots; shock absorbers
Rayleigh (α, β)	PARAM ALPHA1/2	[C] = α[M] + β[K]; use with caution

Typical ζ Values: Welded steel: 0.5-1% | Bolted joints: 1-3% | Composites: 1-2% | Aluminum: 0.2-0.5% | Rubber mounts: 5-15%

Unit Consistency & Critical Parameters

System	Length	Mass	Force	Time	WTMASS
SI	m	kg	N	s	1.0
SI-mm	mm	tonne	N	s	1.0
SI -mm (kg)	mm	kg	mN	s	0.001
English (slinch)	in	slinch	lbf	s	1.0
English (lbm)	in	lbm	lbf	s	1/386.4

WTMASS converts density units: $\rho_{internal} = \text{WTMASS} \times \rho_{input}$

Parameter	Purpose	Recommended
AUTOSPC	Auto-constrain singularities	YES (review .f06 for warnings)
MAXRATIO	Max stiffness ratio check	1.0E7 (default); lower for ill-conditioned
BAILOUT	Stop on singularity	-1 (stop) for debugging
RESVEC	Residual vectors	YES for modal methods with concentrated loads
COUPMASS	Coupled mass matrix	1 for rotational inertia accuracy

Model Simplifications

Non-Structural Mass (NSM)
Add mass without stiffness for paint, insulation, wiring. Use NSM field on PSHELL/PCOMP or CONM2 elements.

Symmetry BCs
Constrain out-of-plane translation and in-plane rotations at symmetry plane. Halves model size.

Mass Lumping (CONM2)
Represent equipment as point masses. Include moments of inertia (I11, I22, I33) for large items.

Substructuring
Use superelements for repeated components or supplier-provided reduced models.

Model Checkout Checklist

Check	Method	What to Look For
Free-Free Modes	SOL 103, no SPCs	6 rigid body modes < 1 Hz (ideally < 0.01 Hz); 7th mode is 1st flex
Mass Properties	GPWG output	Total mass, CG location, MOI vs. CAD/hand calc (within 1-2%)
Strain Energy	ESE output	Identify elements with high strain energy; check for stress concentrations
Grid Point Singularity	AUTOSPC output	Review constrained DOFs; may indicate missing connections
Epsilon Check	EPSILON in .f06	Should be < 1E-8; larger values indicate numerical issues
Max/Min Checks	MAXMIN output	Extreme values may indicate bad elements or units
1g Static Load	SOL 101, GRAV card	Reaction forces = total weight; deflection reasonable

Key Insight: A well-checked model with simple elements often outperforms a complex model with poor mesh quality. Prioritize mesh convergence studies on the first few modes before adding complexity.

Ref: MSC Nastran Linear Static Analysis User's Guide; Cook et al. "Concepts and Applications of Finite Element Analysis" Wiley 2001; NASA-STD-5002 "Structural Design and Test Factors of Safety"; Altair Practical Aspects of FEA

26. Craig-Bampton Component Mode Synthesis

Model reduction technique for efficient dynamic analysis of large, complex assemblies.

Theory Overview

Craig-Bampton (CB) reduces a component's DOFs to boundary DOFs plus a truncated set of fixed-interface normal modes. The transformation preserves dynamic behavior at interfaces while dramatically reducing model size.

Fixed-Interface Normal Modes (Φ)
Eigenvectors from SOL 103 with boundary DOFs fixed (SPC). Capture internal dynamics of component.

Constraint Modes (Ψ)
Static shapes from unit displacement at each boundary DOF. Capture quasi-static coupling between components.

Governing Equations

Original system partitioned into boundary (b) and interior (i) DOFs:

\begin{bmatrix} M_{bb} & M_{bi} \\ M_{ib} & M_{ii} \end{bmatrix} \begin{Bmatrix} \ddot{u}_b \\ \ddot{u}_i \end{Bmatrix} + \begin{bmatrix} K_{bb} & K_{bi} \\ K_{ib} & K_{ii} \end{bmatrix} \begin{Bmatrix} u_b \\ u_i \end{Bmatrix} = \begin{Bmatrix} F_b \\ 0 \end{Bmatrix}

CB transformation matrix:

[T_{CB}] = \begin{bmatrix} I & 0 \\ \Psi & \Phi \end{bmatrix}

where $\Psi = -K_{ii}^{-1}K_{ib}$ (constraint modes) and $\Phi$ = fixed-interface modes

Reduced coordinates: $\{u\} = [T_{CB}]\{q\}$ where $\{q\} = \{u_b, \eta\}^T$

Reduced System:

[\bar{M}]\{\ddot{q}\} + [\bar{K}]\{q\} = \{\bar{F}\}

where $[\bar{M}] = [T_{CB}]^T[M][T_{CB}]$ and $[\bar{K}] = [T_{CB}]^T[K][T_{CB}]$

Implementation in Nastran

Step	Cards/Method	Notes
1. Define Boundary	ASET or BSET	Interface DOFs retained in reduced model
2. Define Modal DOFs	QSET	Generalized coordinates for fixed-interface modes
3. Create Superelement	SESET, BEGIN SUPER	Partition component from residual structure
4. Reduce	SOL 103 with EXTSEOUT	Outputs .op2/.pch with reduced matrices
5. Assemble	ASSIGN SE, SEBULK	Attach reduced component to system model

Key Cards: EIGRL (mode extraction), PARAM EXTOUT (matrix output), DMIG (import reduced matrices)

Residual Vectors

Residual vectors augment the CB basis to improve accuracy for loads not well-represented by truncated modes.

Why Needed:
Truncated modes may miss response to concentrated loads or high-frequency content. Residual vectors span the "missing" subspace.

Implementation:
PARAM RESVEC YES in Nastran. Automatically computes static response to applied loads and orthogonalizes against mode set.

Residual vector for load {F}:

\{r\} = [K]^{-1}\{F\} - \sum_{i=1}^{n} \frac{\{\phi_i\}^T\{F\}}{\omega_i^2} \{\phi_i\}

Captures static response not spanned by retained modes

Modal Truncation Guidelines

Analysis Type	Frequency Cutoff	Rationale
Frequency Response	1.5-2× f_max	Ensures modes near upper frequency are accurate
Transient (shock)	2-3× f_max	Higher modes contribute to peak response
Random Vibration	1.5× f_max	RMS dominated by resonances within band

Mode Participation: Check modal effective mass. Retain modes until cumulative effective mass > 90% in each direction. Low effective mass modes may be truncated even if within frequency range.

Component Coupling

Reduced components are assembled at shared boundary DOFs:

[M_{sys}] = \sum_k [L_k]^T[\bar{M}_k][L_k], \quad [K_{sys}] = \sum_k [L_k]^T[\bar{K}_k][L_k]

where [L_k] = Boolean localization matrix mapping component k boundary DOFs to system DOFs

Interface Compatibility:
Boundary grids must match exactly (location, DOFs). Use SECONCT for non-matching meshes.

Back-Expansion:
Recover interior DOF responses:

\{u_i\} = [\Psi]\{u_b\} + [\Phi]\{\eta\}

Accuracy Verification

Check	Method	Acceptance
Frequency Error	Compare reduced vs. full model modes	< 1% for modes within cutoff
MAC (Modal Assurance)	Correlation of mode shapes	> 0.95 for corresponding modes
FRF Comparison	Point FRF at key locations	Peaks within 5% amplitude, 1% frequency
Static Deflection	Unit load at boundary	< 0.1% error (constraint modes exact for static)

Key Insight: CB reduction is exact for static loads and increasingly accurate as more modes are retained. The constraint modes ensure perfect static response; errors arise only from modal truncation of dynamic content. Always verify with back-expansion at critical locations.

Ref: Craig & Bampton "Coupling of Substructures for Dynamic Analyses" AIAA J. 1968; MSC Nastran Superelement User's Guide; de Klerk et al. "General Framework for Dynamic Substructuring" AIAA J. 2008; Rixen "A Dual Craig-Bampton Method" M2AN 2004

27. Dimensionless Parameters

Dimensionless parameters enable similarity analysis, scaling between test and flight, and characterization of physical phenomena. They are ratios of competing physical effects.

Reynolds Number (Re)

Ratio of inertial forces to viscous forces. Determines flow regime (laminar vs turbulent).

Re = \frac{\rho V L}{\mu} = \frac{V L}{\nu}

$\rho$ = fluid density, $V$ = velocity, $L$ = characteristic length
$\mu$ = dynamic viscosity, $\nu$ = kinematic viscosity

Re Range	Flow Regime	Application
$Re < 2,300$	Laminar (pipe)	Viscous-dominated, predictable
$2,300 < Re < 4,000$	Transitional	Intermittent turbulence
$Re > 4,000$	Turbulent (pipe)	Inertia-dominated, chaotic
$Re_x \approx 5 \times 10^5$	Flat plate transition	Boundary layer transition

Mach Number (M)

Ratio of flow velocity to local speed of sound. Determines compressibility effects.

M = \frac{V}{c} = \frac{V}{\sqrt{\gamma R T}}

$c$ = speed of sound, $\gamma$ = ratio of specific heats (1.4 for air)
$R$ = specific gas constant, $T$ = absolute temperature

Mach Range	Regime	Characteristics
$M < 0.3$	Incompressible	Density changes $< 5\%$ , use Bernoulli
$0.3 < M < 0.8$	Subsonic	Compressibility corrections needed
$0.8 < M < 1.2$	Transonic	Mixed sub/supersonic, shocks form
$1.2 < M < 5$	Supersonic	Shock waves, expansion fans
$M > 5$	Hypersonic	High-temp effects, dissociation

Strouhal Number (St)

Ratio of oscillatory inertia to convective inertia. Characterizes vortex shedding and unsteady flows.

St = \frac{f L}{V}

$f$ = shedding frequency (Hz), $L$ = characteristic length (diameter)
$V$ = flow velocity

Vortex Shedding: For cylinders in crossflow,

St \approx 0.2

over

300 < Re < 2 \times 10^5

. Use to predict lock-in frequencies:

f = St \cdot V / D

Geometry	St Value	Re Range
Circular cylinder	0.18 - 0.22	$300 - 2 \times 10^5$
Square cylinder	0.12 - 0.14	$10^3 - 10^5$
Flat plate (normal)	0.14 - 0.15	$10^4 - 10^5$
Sphere	0.18 - 0.20	$10^3 - 10^5$

Helmholtz Number (He)

Ratio of characteristic length to acoustic wavelength. Determines acoustic compactness.

He = \frac{L}{\lambda} = \frac{f L}{c}

$He \ll 1$ : Acoustically compact (lumped parameter models valid)
$He \approx 1$ : Resonance region (cavity modes, Helmholtz resonators)
$He \gg 1$ : Geometric acoustics (ray tracing valid)

Other Key Parameters

Parameter	Definition	Physical Meaning	Typical Use
Knudsen (Kn)	$Kn = \lambda_{mfp}/L$	Mean free path / length	Continuum vs rarefied flow
Prandtl (Pr)	$Pr = \nu/\alpha = c_p \mu/k$	Momentum / thermal diffusivity	Heat transfer (Pr ≈ 0.7 for air)
Nusselt (Nu)	$Nu = hL/k$	Convective / conductive heat	Heat transfer coefficient
Froude (Fr)	$Fr = V/\sqrt{gL}$	Inertia / gravity	Free surface flows, ships
Weber (We)	$We = \rho V^2 L/\sigma$	Inertia / surface tension	Droplets, sprays, bubbles
Womersley (Wo)	$Wo = L\sqrt{\omega/\nu}$	Unsteady / viscous	Pulsatile flow (blood, hydraulics)
Reduced Freq (k)	$k = \omega c / (2V)$	Unsteadiness parameter	Aeroelasticity, flutter

Knudsen Number Regimes

Kn Range	Regime	Modeling Approach
$Kn < 0.01$	Continuum	Navier-Stokes, no-slip BC
$0.01 < Kn < 0.1$	Slip flow	N-S with slip BC
$0.1 < Kn < 10$	Transitional	DSMC, Boltzmann
$Kn > 10$	Free molecular	Collisionless kinetic theory

Similarity Principle: Two flows are dynamically similar if all relevant dimensionless parameters match. For aeroacoustics: match Re, M, St. For scaling: if geometry scales by

\lambda

, maintain same Re and M to preserve flow physics.

Ref: White "Viscous Fluid Flow" 3rd ed. 2006; Anderson "Fundamentals of Aerodynamics" 6th ed. 2017; Blevins "Flow-Induced Vibration" 2nd ed. 1990; Kinsler et al. "Fundamentals of Acoustics" 4th ed. 2000; Schlichting & Gersten "Boundary-Layer Theory" 9th ed. 2017

28. Acoustic Weighting Scales

Weighting Calculator

Frequency weighting filters adjust measured SPL to approximate human hearing perception or characterize specific noise types. Defined by IEC 61672-1.

Weighting Curves

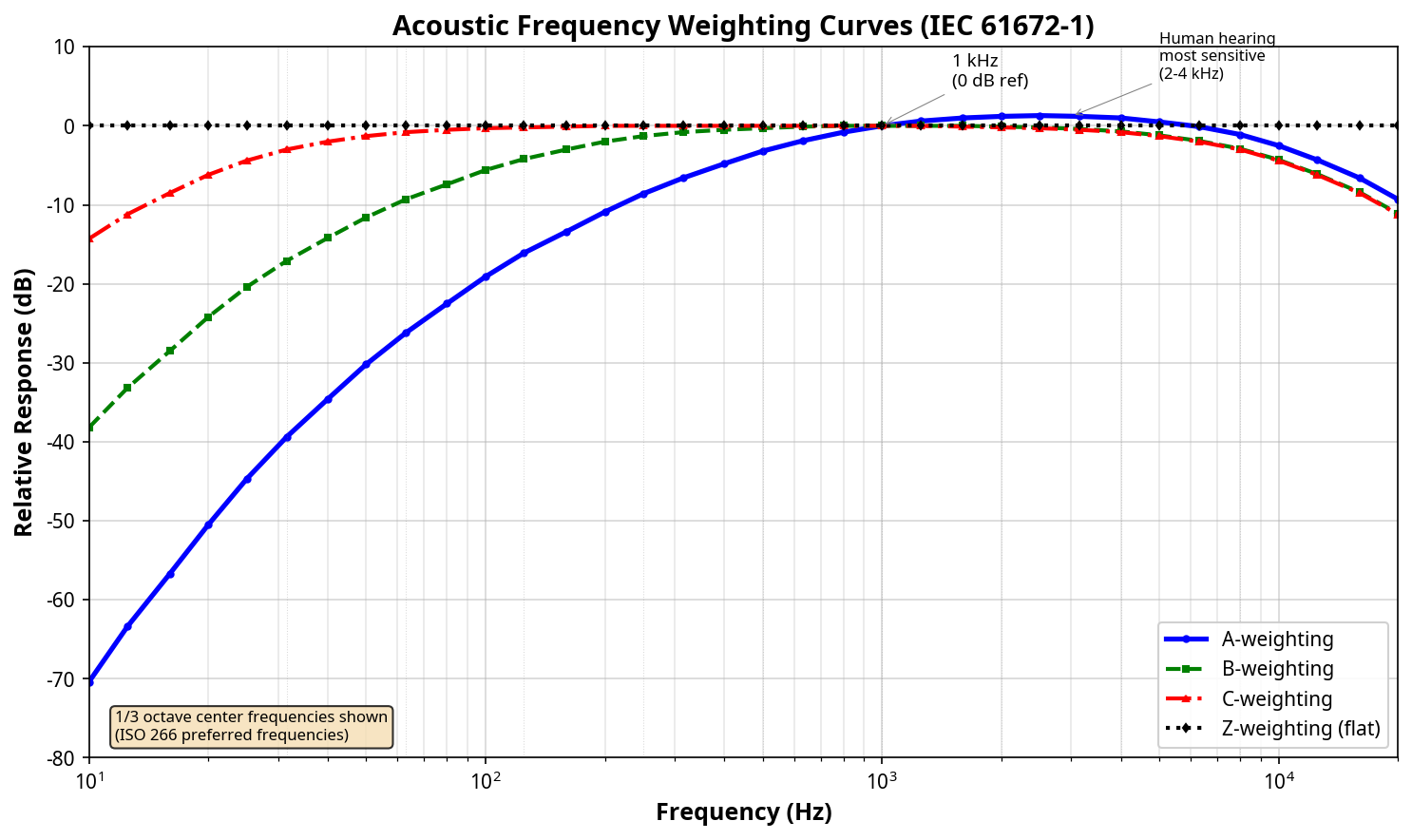
Weighting	Description	Primary Application
A-weighting (dBA)	Approximates 40-phon equal-loudness contour; attenuates low frequencies heavily	Occupational noise, environmental regulations, hearing damage risk
B-weighting (dBB)	Approximates 70-phon contour; moderate low-frequency attenuation	Historical use; largely obsolete (replaced by C)
C-weighting (dBC)	Nearly flat response; slight roll-off at extremes	Peak sound levels, low-frequency noise assessment, C-A difference for LF content
Z-weighting (dBZ)	Flat (unweighted) from 10 Hz to 20 kHz	Engineering measurements, source characterization, research

Octave Band Analysis

Acoustic spectra are typically analyzed in octave or fractional-octave bands per ISO 266.

1/1 Octave Bands

Center frequencies: 31.5, 63, 125, 250, 500, 1k, 2k, 4k, 8k Hz

Bandwidth ratio:

f_2/f_1 = 2

Upper/Lower:

f_u = \sqrt{2} f_c

f_l = f_c/\sqrt{2}

1/3 Octave Bands

Finer resolution (3 bands per octave)

Bandwidth ratio:

f_2/f_1 = 2^{1/3} \approx 1.26

Upper/Lower:

f_u = 2^{1/6} f_c

f_l = f_c/2^{1/6}

Constant Percentage Bandwidth: Octave bands have constant percentage bandwidth (not constant Hz). For 1/3 octave:

\Delta f / f_c = 2^{1/3} - 2^{-1/3} \approx 23\%

. This matches human auditory frequency resolution (critical bands).

A-Weighting Formula

Analytical approximation (IEC 61672-1):

R_A(f) = \frac{12194^2 \cdot f^4}{(f^2 + 20.6^2)(f^2 + 12194^2)\sqrt{(f^2 + 107.7^2)(f^2 + 737.9^2)}}

A(f) = 20\log_{10}(R_A(f)) - 20\log_{10}(R_A(1000)) \text{ dB}

Normalized to 0 dB at 1 kHz. Maximum response ~+1.2 dB near 2.5 kHz.

Key Values at Standard Frequencies

Freq (Hz)	A (dB)	C (dB)	Freq (Hz)	A (dB)	C (dB)
31.5	-39.4	-3.0	500	-3.2	0.0
63	-26.2	-0.8	1000	0.0	0.0
125	-16.1	-0.2	2000	+1.2	-0.2
250	-8.6	0.0	4000	+1.0	-0.8

Overall Sound Pressure Level (OASPL)

Sum of individual band levels using logarithmic (energy) addition:

L_{OA} = 10 \log_{10} \left( \sum_{i=1}^{n} 10^{L_i/10} \right) \text{ dB}

$L_i$ = SPL in each octave band (dB)
$n$ = number of bands

Example: Three bands at 80, 85, 82 dB:

L_{OA} = 10\log_{10}(10^{8.0} + 10^{8.5} + 10^{8.2}) = 10\log_{10}(6.31 \times 10^8) = 87.8 \text{ dB}

Weighted OASPL: Apply A or C weighting corrections to each band before summing to get dBA or dBC overall level.

Ref: IEC 61672-1:2013 "Electroacoustics - Sound level meters"; ISO 266:1997 "Preferred frequencies"; ANSI S1.4-2014 "Sound Level Meters"

29. Noise Criteria (NC) Curves

NC curves are used to rate background noise in occupied spaces, particularly for HVAC system design. Each curve represents a maximum acceptable SPL at each octave band.

NC Curves (ASHRAE)

Determining NC Rating: Plot measured octave band spectrum on NC curves. The NC rating equals the highest NC curve touched or exceeded by any band in the measured spectrum.

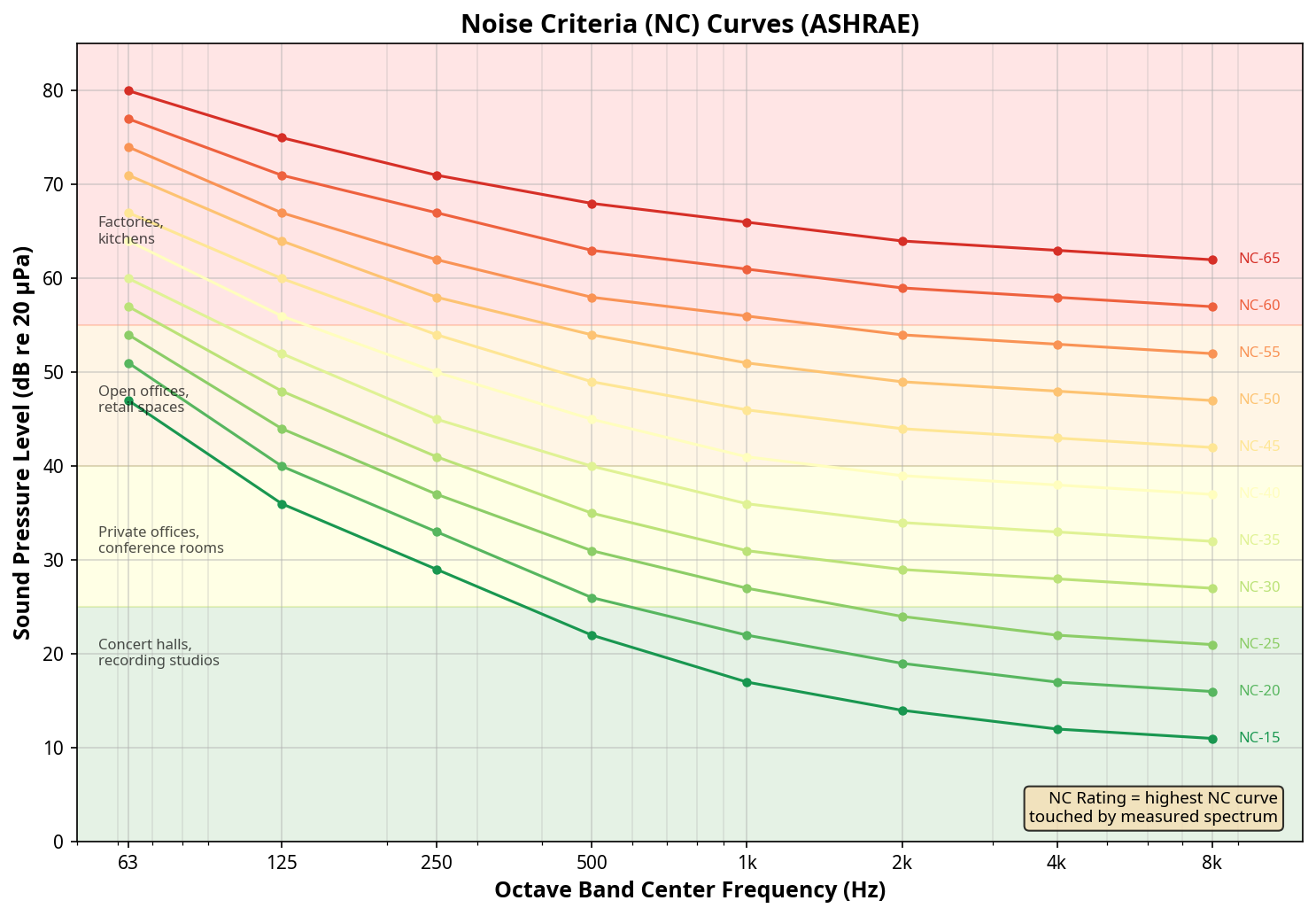
Recommended NC Levels by Space Type

Space Type	NC Range	Notes
Concert halls, recording studios	NC-15 to NC-20	Critical listening environments
Theaters, courtrooms	NC-20 to NC-30	Speech intelligibility critical
Private offices, conference rooms	NC-30 to NC-35	Confidential speech privacy
Open offices, lobbies	NC-35 to NC-45	Normal speech communication
Retail, restaurants	NC-40 to NC-50	Background masking acceptable
Kitchens, laundries, factories	NC-50 to NC-65	High ambient noise expected

Related Rating Systems

RC (Room Criteria)

Improved version addressing rumble (R) and hiss (H) imbalance. Includes quality descriptors.

NR (Noise Rating)

European/ISO equivalent. Similar shape but different values. NR ≈ NC + 5 approximately.

Ref: ASHRAE Handbook - HVAC Applications Ch. 48; ANSI/ASA S12.2-2008 "Criteria for Evaluating Room Noise"; ISO 1996-1 "Acoustics - Description and measurement of environmental noise"

30. Mode Shapes for Beams & Plates

Correlation Visualizer

Mode shapes describe the spatial pattern of vibration at each natural frequency. Understanding mode shapes is essential for predicting structural response to dynamic loads and designing effective vibration control.

1D Beam Mode Shapes (Euler-Bernoulli)

For a uniform beam with bending stiffness EI, mass per unit length ρA, and length L, the mode shapes depend on boundary conditions:

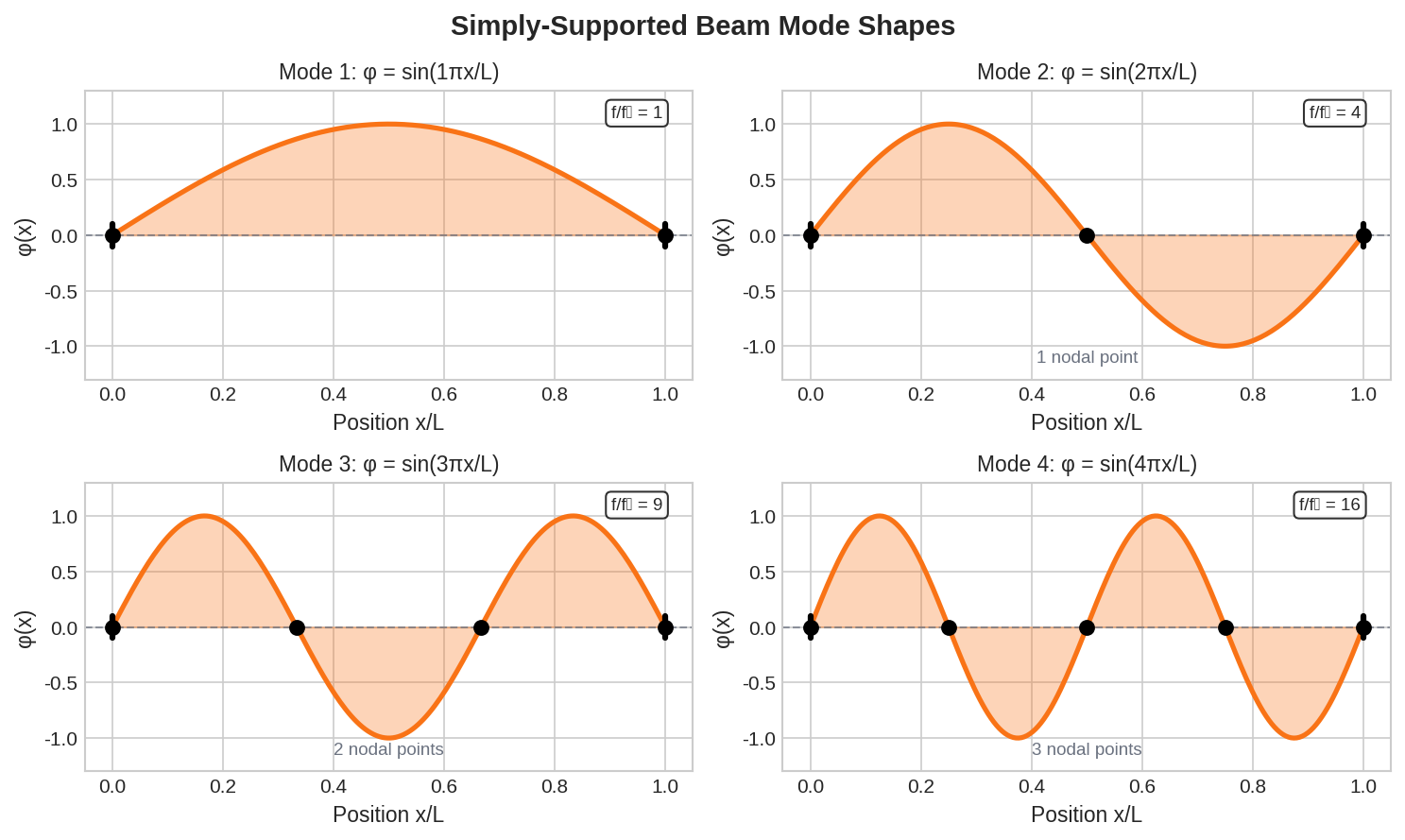
Simply-supported beam: first four mode shapes showing nodal points

Simply-Supported (Pinned-Pinned)

Both ends free to rotate but constrained against translation.

\phi_n(x) = \sin\left(\frac{n\pi x}{L}\right)

f_n = \frac{n^2 \pi}{2L^2} \sqrt{\frac{EI}{\rho A}} = \frac{(n\pi)^2}{2\pi L^2} \sqrt{\frac{EI}{\rho A}}

Symbol	Description	Units
$\phi_n(x)$	Mode shape function (normalized displacement pattern)	dimensionless
$n$	Mode number (1, 2, 3, ...)	integer
$x$	Position along beam	m or in
$L$	Beam length	m or in
$f_n$	Natural frequency of mode n	Hz
$E$	Young's modulus	Pa or psi
$I$	Area moment of inertia	m⁴ or in⁴
$\rho$	Material density	kg/m³ or lb/in³
$A$	Cross-sectional area	m² or in²

Frequency Ratios: f₁ : f₂ : f₃ : f₄ = 1 : 4 : 9 : 16 (proportional to n²)

Clamped-Clamped (Fixed-Fixed)

Both ends constrained against rotation and translation.

\phi_n(x) = \cosh(\beta_n x) - \cos(\beta_n x) - \sigma_n[\sinh(\beta_n x) - \sin(\beta_n x)]

where $\beta_n L$ satisfies $\cos(\beta_n L)\cosh(\beta_n L) = 1$ and $\sigma_n = \frac{\cosh(\beta_n L) - \cos(\beta_n L)}{\sinh(\beta_n L) - \sin(\beta_n L)}$

f_n = \frac{(\beta_n L)^2}{2\pi L^2} \sqrt{\frac{EI}{\rho A}}

Mode n	$\beta_n L$	Freq. Ratio (rel. to SS mode 1)
1	4.730	2.27
2	7.853	6.27
3	10.996	12.24
4	14.137	20.25

Cantilever (Fixed-Free)

One end clamped, other end free.

\phi_n(x) = \cosh(\beta_n x) - \cos(\beta_n x) - \sigma_n[\sinh(\beta_n x) - \sin(\beta_n x)]

where $\beta_n L$ satisfies $\cos(\beta_n L)\cosh(\beta_n L) = -1$

Mode n	$\beta_n L$	Freq. Ratio (rel. to SS mode 1)
1	1.875	0.356
2	4.694	2.23
3	7.855	6.27
4	10.996	12.24

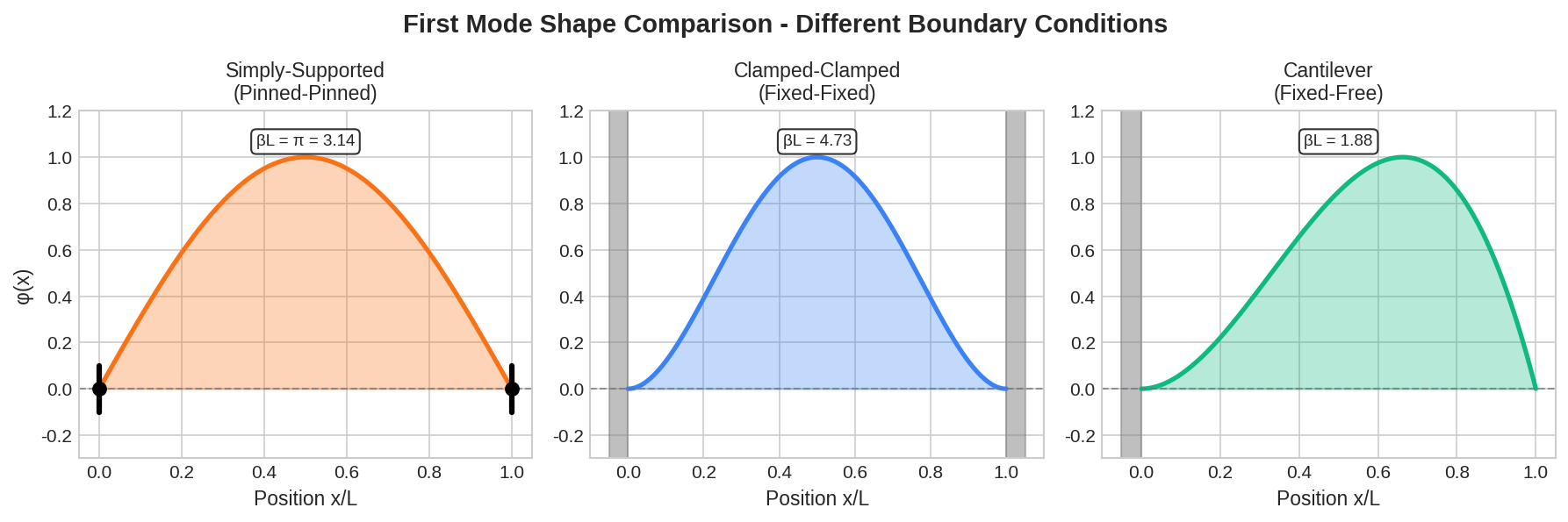
First Mode Shape Comparison - Different Boundary Conditions

First mode shape comparison: boundary conditions significantly affect both shape and frequency

2D Rectangular Plate Mode Shapes

For a thin, isotropic rectangular plate with dimensions a × b, thickness h, and simply-supported edges:

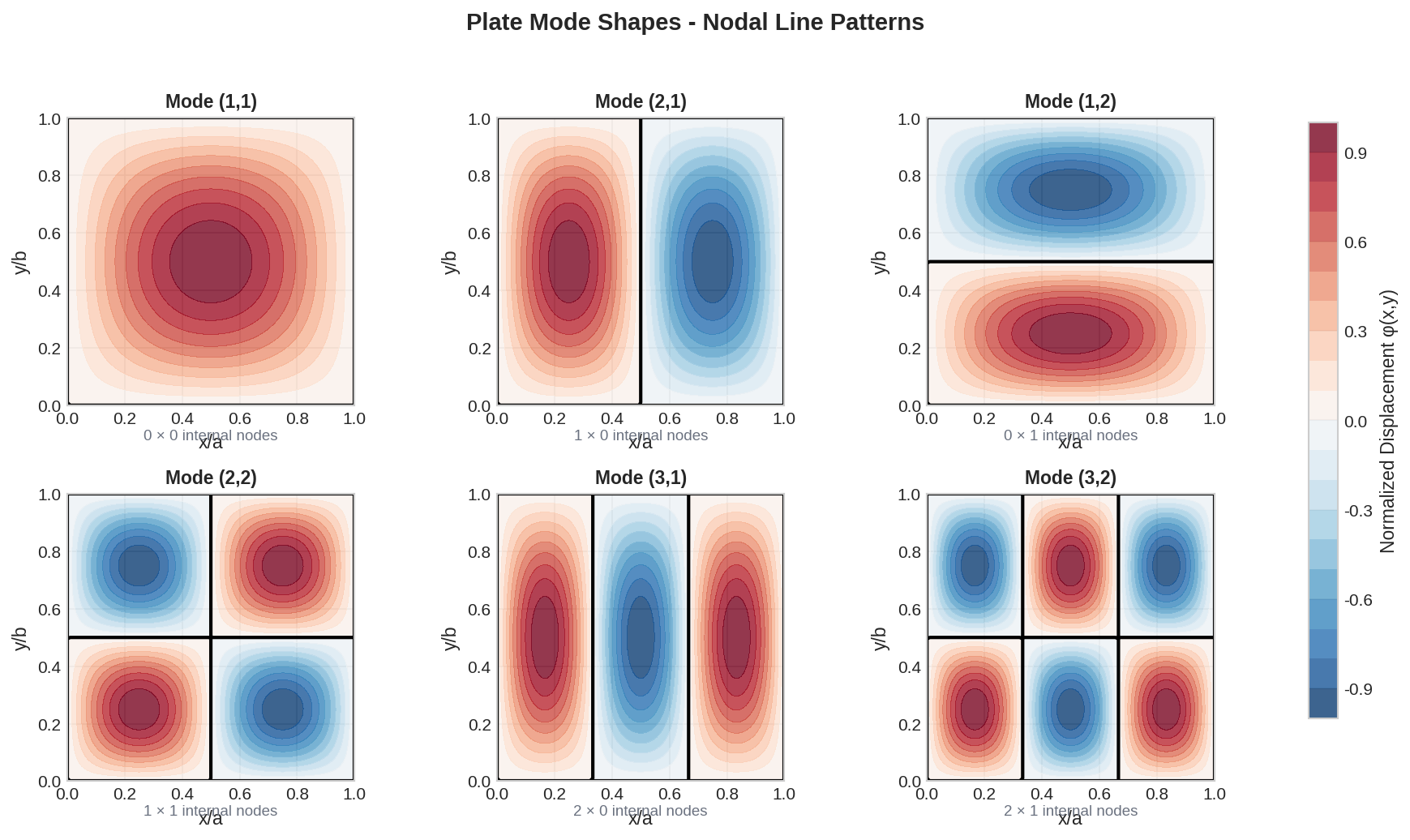
Simply-supported plate mode shapes showing nodal lines (black) where displacement is zero

Simply-Supported Plate (All Edges)

\phi_{mn}(x,y) = \sin\left(\frac{m\pi x}{a}\right) \sin\left(\frac{n\pi y}{b}\right)

f_{mn} = \frac{\pi}{2} \sqrt{\frac{D}{\rho h}} \left[\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2\right]

D = \frac{Eh^3}{12(1-\nu^2)}

Symbol	Description	Units
$\phi_{mn}(x,y)$	Mode shape function for mode (m,n)	dimensionless
$m, n$	Mode indices in x and y directions (1, 2, 3, ...)	integers
$a, b$	Plate dimensions in x and y	m or in
$h$	Plate thickness	m or in
$D$	Flexural rigidity (bending stiffness)	N·m or lb·in
$\nu$	Poisson's ratio	dimensionless
$f_{mn}$	Natural frequency of mode (m,n)	Hz

Mode Shape Notation

Plate modes are identified by (m,n) where m = half-waves in x-direction, n = half-waves in y-direction:

(1,1)
Fundamental

(2,1)
1 nodal line in x

(1,2)
1 nodal line in y

(2,2)
Cross pattern

Square Plate Frequency Ratios (a = b)

Mode (m,n)	Frequency Ratio	Nodal Pattern
(1,1)	1.00	No internal nodes
(2,1) or (1,2)	2.50	1 nodal line
(2,2)	4.00	Cross pattern
(3,1) or (1,3)	5.00	2 nodal lines parallel
(3,2) or (2,3)	6.50	Mixed pattern
(3,3)	9.00	Grid pattern

Key Concepts

Nodal Lines/Points

Locations where displacement is zero for a given mode. Higher modes have more nodal lines.

Modal Wavenumber

$k_m = n\pi/L$ for beams. Determines spatial frequency of mode shape.

Orthogonality

Mode shapes are orthogonal: $\int \phi_m \phi_n \, dx = 0$ for m ≠ n. Enables modal superposition.

Mass Normalization

Modes often normalized so $\int \rho A \phi_n^2 \, dx = 1$ (unit modal mass).

Ref: Blevins "Formulas for Dynamics, Acoustics and Vibration" Wiley 2016, Tables 7-1 through 7-4; Leissa "Vibration of Plates" NASA SP-160 1969; Rao "Mechanical Vibrations" Pearson 2017, Ch. 8

Designed for professional reference. Verify all safety-critical calculations.

01. Core Acoustics & dB Fundamentals

Sound Pressure Level (SPL)

Wave Equation

02. SDOF Dynamics

Dynamic Magnification Factor (DMF)

Phase Angle (ϕ\phiϕ)

Transmissibility

03. Damping Types

Viscous Damping

Structural (Hysteretic) Damping

Coulomb (Dry Friction) Damping

Q Factor & Loss Factor

04. MDOF Dynamics

Matrix Equation of Motion

Eigenvalue Problem (Free Vibration)

Modal Superposition

Modal Vector Interpretation

05. Force Balance (Beam Theory)

Relationships

Force/Moment Balance

Boundary Conditions

06. Random Vibration

Miles' Equation

G-RMS from PSD

07. Vibration Statistics

Distributions

Sigma (σ\sigmaσ) Peaks

08. VRS & Extreme Response Spectrum

Vibration Response Spectrum (VRS)

Extreme Response Spectrum (ERS)

09. Acoustic Source Models & Correlation

Acoustic Sources

What is Spatial Correlation?

Turbulent Boundary Layer (TBL)

TBL Correlation: Corcos Model

Diffuse Acoustic Field (DAF)

DAF Spatial Correlation

Correlation Comparison

10. Room Acoustics

Reverberation Time (T60)

Absorption & Room Constant

11. Statistical Energy Analysis (SEA)

Power Balance Equation

12. FEA & NASTRAN Dynamics

Solution Sequences (SOL)

DOF Sets (Matrix Reduction)

13. FEA Mesh Guidelines

Elements per Wavelength

Wave Types & Speeds

Critical Bending Wavelength

14. DSP & Data Acquisition

Sampling & Aliasing

Dynamic Range & Bit Depth

Window Functions

15. Vibroacoustics Scaling Techniques

Franken Method

Barrett Scaling

Q-Scaling (SPL)

16. Sensor Selection Guide

Accelerometer Types

Selection Criteria

17. Structural Engineering Fundamentals

Static Equilibrium

Free Body Diagram (FBD) Checklist

Support Reactions

Internal Forces

18. Cylinders, Rings, Shells & Cones

Ring Frequency

Critical (Coincidence) Frequency

Shell Behavior Regimes

Circumferential Mode Shapes

Radiation Efficiency

Ring Stiffener Effects

19. Aerospace Material Properties

Common Aerospace Materials (Metric)

Common Aerospace Materials (English)

20. Rotating Dynamics

Campbell Diagram

Blade Mode Stiffening

Excitation Lines

Phase Angle ( $\phi$ )

Sigma ( $\sigma$ ) Peaks